Szereg Fouriera

Szereg Fouriera – szereg pozwalający rozłożyć funkcję okresowąSzablon:Odn lub nieokresowąSzablon:Odn, spełniającą warunki Dirichleta, na sumę funkcji trygonometrycznych. Szeregi Fouriera zostały wprowadzone w 1807 roku przez Josepha Fouriera w celu rozwiązania równania przewodnictwa ciepła dla metalowej płyty. Równanie to jest równaniem różniczkowym cząstkowym i nie da się go rozwiązać bezpośrednio dla większości funkcji; jednak rozkładając funkcję początkową na szereg Fourier łatwo znalazł rozwiązania równania przewodnictwa dla poszczególnych składowych harmonicznych, ponieważ pochodne funkcji trygonometrycznych dają proste wzory, a następnie obliczył rozwiązanie dla funkcji wejściowej, sumując rozwiązania dla jej składowych harmonicznych. W 1829 r. Dirichlet określił ściśle warunki, jakie muszą spełniać funkcje, by szereg Fouriera był do nich zbieżny.

Szeregi Fouriera są np. ściśle powiązane z transformatą Fouriera, odkrytą przez Fouriera, którą można wykorzystać do znalezienia informacji o częstotliwościach składowych funkcji nieokresowych.

Od czasów Fouriera odkryto wiele różnych podejść do definiowania i rozumienia szeregu Fouriera. Niektóre z bardziej wydajnych i eleganckich podejść opierają się na pomysłach i narzędziach matematycznych, które nie były dostępne w czasach Fouriera. Fourier pierwotnie zdefiniował szereg Fouriera dla funkcji argumentów rzeczywistych o wartościach rzeczywistych i użył funkcji sinus i cosinus w dekompozycji. Od tego czasu zdefiniowano wiele innych transformacji, rozszerzając jego początkowy pomysł na wiele zastosowań i tworząc dział matematyki zwany analizą Fourierowską.

Metoda Fouriera doprowadziła do przewrotu w matematyce i zainicjowała powstanie wielu nowych teorii. Dziś szeregi Fouriera mają wielkie znaczenie między innymi w fizyce, teorii drgań oraz przetwarzaniu sygnałów obrazu (kompresja jpeg) i dźwięku (kompresja mp3).

Definicje szeregu Fouriera

Definicja za pomocą funkcji sin i cosSzablon:Odn

Niech dana będzie funkcja okresowa $f:ℝ\to ℝ$ o okresie $T>0,$ bezwzględnie całkowalna w przedziale $[\frac{-T}{2},\frac{T}{2}]$. Trygonometrycznym szeregiem Fouriera funkcji $f$ nazywamy szereg funkcyjny postaci

o współczynnikach określonych wzorami:Szablon:Wzór

Szablon:Wzór

Powyższe wzory po raz pierwszy opublikował Jeana-Baptiste Joseph Fourier. Niemniej jednak po raz pierwszy wyprowadził je Leonhard Euler (prac na ten temat nie opublikował). Wzory te noszą nazwę wzorów Eulera-Fouriera.

Wprowadzając dla uproszczenia oznaczenie $\omega =\frac{2\pi }{T}$ w powyższych wzorach, gdzie $\omega$ to tzw. pulsacja lub częstość kołowa, otrzymamy:Szablon:Wzór

Szablon:Wzór

Szablon:Wzór

Definicja za pomocą funkcji zespolonychSzablon:Odn

Niech dana będzie funkcja okresowa $f:ℝ\to ℝ$ o okresie $T>0$ bezwzględnie całkowalna w przedziale $[-\frac{T}{2},\frac{T}{2}]$. Zespolonym szeregiem Fouriera funkcji $f$ nazywamy szereg funkcyjny

$S(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n{e}^{in\omega x}$

gdzie

$c_n=\frac{1}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)e^{-in\omega x}dx$

Związek między współczynnikami rozwinięcia trygonometrycznego i zespolonego

$c_n=\{\begin{array}{cccc}& \frac{1}{2}(a_n-i{b}_n)& & \text{gdy}n>0\\ & \frac{1}{2}{a}_0& & \text{gdy}n=0\\ & \frac{1}{2}(a_{-n}+i{b}_{-n})& & \text{gdy}n<0\end{array}$

Obliczanie szeregu Fouriera funkcji nieciągłej. Twierdzenie Dirichleta

Wykres funkcji piłokształtnej, która składa się z powtórzeń funkcji $s(x)=x/\pi$ określonej na przedziale $(-\pi ,\pi >$.

Animacja pięciu kolejnych wyrazów szeregu Fouriera aproksymującego funkcję piłokształtną

Rozważmy funkcję piłokształtną:

$\{\begin{array}{cccc}& s(x)=\frac{x}{\pi }& & -\pi <x<\pi ,\\ & s(x+2\pi k)=s(x),& & -\pi <x<\pi ,k=0,\pm 1,\pm 2,\dots \end{array}$

Obliczając jej współczynniki szeregu Fouriera otrzymamy:

$a_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}s(x)\cos (nx)dx=0,n\ge 0$

$b_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}s(x)\sin (nx)dx,n\ge 1$

$b_n=-\frac{2}{\pi n}\cos (n\pi )+\frac{2}{{\pi }^2{n}^2}\sin (n\pi )$

i ostatecznie

$b_n=\frac{2(-1{)}^{n+1}}{\pi n},n\ge 1$

Można pokazać, że szereg Fouriera zbiega do funkcji $s(x)$ we wszystkich punktach $x$, w których funkcja $s$ jest ciągła, tj.

Wykres funkcji signum, w punkcie x=0 nieciągłej w sposób odosobniony, nieusuwalny i pierwszego rodzaju (zwyczajny).

$\begin{array}{cc}S(x)& =\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos \left(nx\right)+b_n\sin \left(nx\right)]\\ & =\frac{2}{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}\sin (nx),\mathrm{d}\mathrm{l}\mathrm{a}x\ne \pm \pi ,\pm 3\pi ,\pm 5\pi ,\dots \end{array}$

Dla $x=\pi$ (i ogólnie dla $x=\pm \pi ,\pm 3\pi ,\pm 5\pi ,\dots$) szereg Fouriera zbiega do wartości 0. Wartość ta jest równa połowie sumy wartości granic lewo- i prawostronnych funkcji $s(x)$ w punkcie $x=\pi$. W punkcie $x=\pi$ funkcja nie została zdefiniowana. Jeżeli więc chcielibyśmy, by szereg był zbieżny do funkcji $s(x)$ w tym punkcie (i ogólnie dla $x=\pm \pi ,\pm 3\pi ,\pm 5\pi ,\dots$), to należałoby uzupełnić jej definicję przyjmując:

$\{\begin{array}{cccc}& s(x)=\frac{x}{\pi }& & -\pi <x<\pi ,\\ & s(x+2\pi k)=s(x),& & -\pi <x<\pi ,k=0,\pm 1,\pm 2,\dots \\ & s(x)=0,& & x=\pm \pi ,\pm 3\pi ,\pm 5\pi ,\dots \end{array}$

Wniosek ten jest zawarty w twierdzeniu Dirichleta, które orzeka, iżSzablon:Odn

Jeżeli funkcja jest w przedziale $-\frac{T}{2}<x<\frac{T}{2}$ ograniczona i ciągła lub posiada nieciągłości najwyższej 1-go rodzaju (tj. spełniające warunek: w punkcie nieciągłości istnieją granice funkcji lewo- i prawostronna) i w skończonej liczbie, to (1) szereg Fouriera zbiega do funkcji w punktach ciągłości (2) w punktach nieciągłości szereg zbiega do wartości równej połowie sumy granic lewo- i prawostronnej funkcji w tych punktach.

Uwaga 1: Z powyższego przykładu widać, że funkcja rozwijana w szereg Fouriera może nie być zdefiniowana w punktach nieciągłości 1-go rodzaju - brak wartości funkcji w tych punktach nie przeszkadza w obliczaniu współczynników Fouriera $a_n,b_n,$ ani nie ma wpływu na ich wartość (bowiem wartości całek nie zależą od wartości funkcji na zbiorze miary zero, a takiej miary jest zbiór punktów nieciągłości funkcji).

Uwaga 2: Powyższy przykład prowadzi do rozwiązania tzw. problemu bazylejskiego.

Funkcja nieokresowa $s(x)$ o dziedzinie $[0,L]$ i generowany przez nią szereg Fouriera $S(x)$

Szereg Fouriera funkcji nieokresowej

Funkcję nieokresową $s(x)$, określoną dla $x\in [-\frac{L}{2},\frac{L}{2}]$ można rozwinąć w szereg Fouriera, obliczając współczynnika Fouriera jak dla funkcji okresowej o okresie $T=L$. Szereg Fouriera jest zawsze funkcją okresową, nawet jeśli oryginalna funkcja $s(x)$ nią nie jest. Jednak ograniczając się do wartości szeregu dla $x\in [-\frac{L}{2},\frac{L}{2}]$ otrzymamy rozkład oryginalnej funkcji na szereg Fouriera.

Funkcja $s(x)$ musi przy tym spełniać na przedziale zmienności te same warunki ograniczoności i ciągłości, co funkcja okresowa na przedziale $T=L$.

Uwaga:

Jeżeli funkcja $f(x)$ jest okresowa, to rozwinięcia w szereg Fouriera można dokonać na dowolnym przedziale $x\in [-\frac{L}{2}+x_0,\frac{L}{2}+x_0]$, gdzie $x_0$ - dowolne przesunięcie powyższego zakresu; np. dla $x\in [0,L]$. Wtedy wystarczy obliczać całki na współczynniki rozwinięcia w innym zakresie.Szablon:Odn Analogicznie dotyczy to rozwinięć funkcji nieokresowych na innych przedziałach zmienności zmiennej $x.$

Dokładność aproksymacji funkcji szeregiem Fouriera. Efekt Gibbsa

Twierdzenie nt. dokładności aproksymacji

Tw. Przy zastąpieniu funkcji $f(x)$ przybliżoną sumą trygonometryczną

$S_N(x)=\frac{a_0}{2}+\sum _{n=1}^N[a_n\cos (nx)+b_n\sin (nx)]$

średni błąd kwadratowy

${\delta }^2=\frac{1}{T}\underset{-T/2}{\overset{T/2}{\int }}[f(x)-S_N(x){]}^{2}dx$

jest najmniejszy, jeżeli za współczynniki $a_n,b_n$ przyjmie się współczynniki Fouriera funkcji $f(x)$ Szablon:Odn.

Przykład

Zależność $\theta (t)$ położenia kątowego wahadła od czasu (drgania silnie nieliniowe; amplituda 179.98°; niebieski) oraz przybliżenie sumą częściową szeregu Fouriera (niebieski przerywany) i rozwiązaniem $\theta (t{)}_{\text{Maclaurin-3}}$, w którym człon nieliniowy $\sin \theta (t)$ równania wahadła przybliżono do trzeciego wyrazu szeregu Maclaurina.

Powyższe twierdzenie orzeka, iż spośród wszystkich funkcji, przybliżających daną funkcję za pomocą skończonej kombinacji liniowej funkcji sinusoidalnych i kosinusoidalnych najmniejszy średni błąd kwadratowy uzyska się dla współczynników będących współczynnikami rozwinięcia danej funkcji w szereg Fouriera. Dla ilustracji pokazano tu przybliżenia funkcji

$\theta (t)$

(opisującej kat odchylania wahadła matematycznego od pionu) za pomocą dwóch funkcji o identycznych składowych harmonicznych, ale o różnych współczynnikach

(a) przybliżenie sumą częściową $S_3$ szeregu Fouriera funkcji $\theta (t)$

$S_3(t)=b_1\cdot \sin (\omega t)+b_3\cdot \sin (3\omega t)$,

(b) przybliżenie funkcją $\theta (t{)}_{\text{Maclaurin-3}}$, która jest rozwiązaniem przybliżenia równania nieliniowego ruchu wahadła za pomocą rozwinięcia w szereg Maclaurina członu nieliniowego tego równania:

$\theta (t{)}_{\text{Maclaurin-3}}=({\theta }_0+\frac{{\theta }_0^3}{192})\cdot \sin (\omega t)+\frac{{\theta }_0^3}{192}\cdot \sin (3\omega t),$

gdzie:

• ${\theta }_0$ - amplituda drgań wahadła,
• $\omega =2\pi /T$, gdzie $T({\theta }_0)=4\sqrt{\frac{\ell }{g}}\cdot K(\sin \frac{{\theta }_0}{2})$ - okres drgań wahadła, słuszny dla dowolnych amplitud,
• $K$ - całka eliptyczna zupełna pierwszego rodzaju

Z obliczeń średniego błędu kwadratowego otrzymano:

(a) dla $S_3$: ${\delta }^2\approx 390$

(a) dla ${\theta }_{\text{Maclaurin-3}}$: ${\delta }^2\approx 2201$

Zwiększenie liczby wyrazów w liczeniu sumy częściowej Fouriera zmniejsza średni błąd kwadratowy; dla

$S_{100}$

otrzymuje się

${\delta }^2=4\cdot 10^{-21}\approx 0$

. Widać stąd, iż analiza Fouriera stanowi skuteczne narzędzie znajdowania znakomitych aproksymacji rozwiązań równań różniczkowych.

• 
  Cztery sumy częściowe szeregu Fouriera zawierające 1, 2, 3 i 4 wyrazy, pokazujące, jak poprawia się przybliżenie funkcji prostokątnej ze wzrostem liczby wyrazów (tu dokładna animacja)
• 
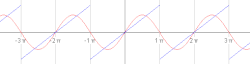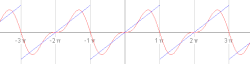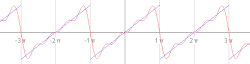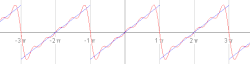
  Cztery sumy częściowe szeregu Fouriera zawierające 1, 2, 3 i 4 wyrazy, pokazujące, jak poprawia się przybliżenie funkcji piłokształtnej ze wzrostem liczby wyrazów (tu dokładna animacja)

Efekt Gibbsa tj. powstawanie oscylacji o dużych amplitudach sum Fouriera w punktach nieciągłości funkcji aproksymowanej (pionowe odcinki wykresu).

Zależność aproksymacji od liczby wyrazów sumy aproksymującej

Dokładność aproksymacji danej funkcji za pomocą szeregu Fouriera zależy od liczby wyrazów N szeregu - im więcej wyrazów sumy częściowej, tym mniejszy jest średni błąd kwadratowy. Pokazują to poniższe animacje.

Efekt Gibbsa

Dla funkcji nieciągłych pojawia się tzw. efekt Gibbsa w aproksymacji - w punktach nieciągłości (odcinki skoków pionowych) następują silne odchylenia funkcji aproksymującej od wartości średniej, pomimo że maleje średni błąd kwadratowy aproksymacji danej funkcji za pomocą sum częściowych

$S_N$

szeregu Fouriera wraz ze wzrostem liczby

$N$

wyrazów sumy aproksymującej. W związku z tym stosuje się różne techniki wygładzania lokalnego funkcji aproksymującej w pobliży punktów nieciągłości.

Funkcja $s_6(x)$ (czerwona) to suma 6 funkcji sinus (niebieskie) i funkcja $S(f)$ ich amplitud $b_n$.

Widmo czyli amplitudy składowych harmonicznych

Współczynniki szeregu Fouriera $a_n,b_n$ reprezentują amplitudy składowych harmonicznych $\cos (n\omega x),\sin (n\omega x)$, jakie zawiera dany sygnał. Zbiór tych współczynników nazywa się widmem danej funkcji.

Animacja obok pokazuje widmo funkcji, która ma jedynie składowe sinusoidalne widma.

Dalej pokazano widmo dla ogólnego przypadku.

Funkcja $f(x)=x^2-0.1*x^3$, jej funkcja aproksymująca - suma $N=20$ wyrazów szeregu Fouriera oraz widmo czyli zestaw współczynników $a_n,b_n$

Obliczenia numeryczne szeregu Fouriera

Poniżej podano kod programu w języku Python, który dla danej funkcji $f(x)$ liczy współczynniki szeregu Fouriera $a_n,b_n$, oblicza funkcję aproksymującą funkcję wyjściową, rysuje funkcję daną i aproksymującą oraz rysuje widmo składowych harmonicznych, którego wartości są równe wartościom składowych szeregu Fouriera.

Użytkownik może ustalić:

1. Parametr $L$ określający zakres $[-L,L]$, na którym jest zdefiniowana funkcja, taki że $T=2L$ (linia 9 kodu)
2. Liczbę $N$ wyrazów funkcji aproksymującej (linia nr 10)
3. Definicję funkcji $f(x)$ (linia nr 14)
4. Program można testować, korzystając np. z darmowego notatnika colab google online.

# JK 2024.08.16 v.1 Program oblicza współczynniki szeregu Fouriera danej funkcji,
# rysuje wykres funkcji i funkcji aproksymujacej, rysuje wykres widma

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad

# Parametry
L = np.pi  # Okres (od -L do L)
N = 10     # Liczba wyrazów w szeregu Fouriera

# Definicja funkcji f(x) = x
def f(x):
    return x*x-0.5*x**3

# Współczynniki a_n i b_n
a0 = (1 / L) * quad(f, -L, L)[0]

def a_n(n):
    integrand = lambda x: f(x) * np.cos(n * np.pi * x / L)
    result, _ = quad(integrand, -L, L)
    return result / L

def b_n(n):
    integrand = lambda x: f(x) * np.sin(n * np.pi * x / L)
    result, _ = quad(integrand, -L, L)
    return result / L

# Funkcja rekonstrukcji z szeregu Fouriera
def fourier_series(x, N):
    a0_term = a0 / 2
    sum_terms = sum(a_n(n) * np.cos(n * np.pi * x / L) + b_n(n) * np.sin(n * np.pi * x / L) for n in range(1, N + 1))
    return a0_term + sum_terms

# Zakres x dla wykresu
x_values = np.linspace(-L, L, 500)
f_values = f(x_values)
fs_values = [fourier_series(x, N) for x in x_values]

# Obliczanie współczynników dla widma
n_values = np.arange(1, N + 1)
a_n_values = np.array([a_n(n) for n in n_values])
b_n_values = np.array([b_n(n) for n in n_values])

# Wykres funkcji i szeregu Fouriera
plt.figure(figsize=(14, 6))

# Wykres funkcji i szeregu Fouriera
plt.subplot(1, 2, 1)
plt.plot(x_values, f_values, label="f(x) = x*x-0.5*x**3", color="blue")
plt.plot(x_values, fs_values, label=f"Szereg Fouriera, N = {N}", color="red", linestyle="--")
plt.title("Funkcja f(x) i jej szereg Fouriera")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)

# Wykres widma Fouriera
plt.subplot(1, 2, 2)
plt.stem(n_values, np.abs(a_n_values), linefmt='b-', markerfmt='bo', basefmt='b-', label='a_n')
plt.stem(n_values, np.abs(b_n_values), linefmt='r-', markerfmt='ro', basefmt='r-', label='b_n')
plt.title("Widmo Fouriera")
plt.xlabel("n")
plt.ylabel("Amplituda")
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

Twierdzenia o rozwinięciu funkcji w szereg Fouriera

Aproksymacja funkcji prostokątnej szeregiem Fouriera; N=50. Widoczny efekt Gibbsa w punktach skoków funkcji

Aproksymacja funkcji piłokształtnej szeregiem Fouriera; N=50. Widoczny efekt Gibbsa w punktach skoków funkcji

Aproksymacja funkcji trójkątnej szeregiem Fouriera; N=25. Tu brak efektu Gibbsa, gdyż funkcja nie ma punktów nieciągłości.

Podane tu dwa zasadnicze twierdzenia dotyczą warunków rozwinięcia za pomocą szeregu Fouriera funkcji okresowej. Zakładamy, że funkcja ma okres $T$ i pulsację $\omega =\frac{2\pi }{T}.$ Twierdzenia poprzedzone są lematami, potrzebnymi do ich dowodów.

Lemat I (całki pomocnicze)

• $n$ jest liczbą całkowitą

$\underset{-T/2}{\overset{T/2}{\int }}\cos n\omega xdx=\{\begin{array}{cccc}& 0& & \text{gdy}n\ne 0\\ & T& & \text{gdy}n=0\end{array}$

$\underset{-T/2}{\overset{T/2}{\int }}\sin n\omega xdx=0$

• $m,n$ są liczbami naturalnymi

$\underset{-T/2}{\overset{T/2}{\int }}\cos n\omega x\cdot \cos m\omega xdx=\{\begin{array}{cccc}& 0& & \text{gdy}n\ne m\\ & \frac{T}{2}& & \text{gdy}n=m\end{array}$

$\underset{-T/2}{\overset{T/2}{\int }}\sin n\omega x\cdot \sin m\omega xdx=\{\begin{array}{cccc}& 0& & \text{gdy}n\ne m\\ & \frac{T}{2}& & \text{gdy}n=m\end{array}$

$\underset{-T/2}{\overset{T/2}{\int }}\sin n\omega x\cdot \cos m\omega xdx=0$

Lemat II

$\frac{1}{2}+\sum _{n=1}^N\cos n\alpha =\frac{\sin (N+\frac{1}{2})\alpha }{2\sin \frac{1}{2}\alpha }$

Dowód

$\begin{array}{cc}& \frac{1}{2}+\sum _{n=1}^N\cos n\alpha \\ =& \mathrm{\Re }(-\frac{1}{2}+\sum _{n=0}^N{e}^{in\alpha })\\ =& \mathrm{\Re }(-\frac{1}{2}+\frac{1-e^{i(N+1)\alpha }}{1-e^{i\alpha }})\\ =& -\frac{1}{2}+\frac{1}{|1-e^{i\alpha }{|}^2}\mathrm{\Re }((1-e^{i(N+1)\alpha })(1-e^{-i\alpha }))\\ =& -\frac{1}{2}+\frac{1}{(1-\cos \alpha {)}^2+{\sin }^2\alpha }\mathrm{\Re }(1-e^{-i\alpha }-e^{i(N+1)\alpha }+e^{iN\alpha })\end{array}$

więc mamy (biorąc cześć rzeczywistą i stosując podstawowe wzory trygonometryczne):

$\begin{array}{cc}& \frac{1}{2}+\sum _{n=1}^N\cos n\alpha \\ =& -\frac{1}{2}+\frac{1-\cos \alpha -\cos (N+1)\alpha +\cos N\alpha }{2(1-\cos \alpha )}\\ =& \frac{\cos N\alpha -\cos (N+1)\alpha }{2(1-\cos \alpha )}\\ =& \frac{2\sin (N+\frac{1}{2})\alpha \sin \frac{1}{2}\alpha }{4{\sin }^2\frac{1}{2}\alpha }\\ =& \frac{\sin (N+\frac{1}{2})\alpha }{2\sin \frac{1}{2}\alpha }\end{array}$

q. e. d.

Lemat III

Jeżeli $f$ jest funkcją ciągłą w przedziale $[a,b]$ z wyjątkiem co najwyżej skończonej ilości punktów i bezwzględnie całkowalną w tym przedziale to

$\underset{n\to \mathrm{\infty }}{\lim }\underset{a}{\overset{b}{\int }}f(x)\sin nx\text{d}x=0$

Twierdzenie (Eulera–Fouriera)

Jeżeli szereg o postaci Szablon:LinkWzór jest jednostajnie zbieżny do funkcji $f$ to współczynniki $a_k,b_k$ wyrażają się wzorami Szablon:LinkWzór, Szablon:LinkWzór.

Dowód

$f(x)=\frac{a_0}{2}+\sum _{k=1}^{\mathrm{\infty }}(a_k\cos k\omega x+b_k\sin k\omega x)$

Mnożąc powyższą równość przez $\cos n\omega x,$ całkując szereg w granicach od $-\frac{T}{2}$ do $\frac{T}{2}$ (uwzględniając zbieżność jednostajną szeregu stosujemy twierdzenie o całkowaniu szeregu wyraz po wyrazie) otrzymujemy:

$\underset{-T/2}{\overset{T/2}{\int }}f(x)\cos n\omega x\text{d}x=\frac{a_0}{2}\underset{-T/2}{\overset{T/2}{\int }}\cos n\omega x\text{d}x+\sum _{k=1}^{\mathrm{\infty }}(a_k\underset{-T/2}{\overset{T/2}{\int }}\cos n\omega x\cdot \cos k\omega x\text{d}x+b_k\underset{-T/2}{\overset{T/2}{\int }}\cos n\omega x\cdot \sin k\omega x\text{d}x)$

Na mocy lematu I zerują się wszystkie całki po prawej stronie takie że $n\ne k$ (gdy $n=0$ zeruje się cała suma uogólniona). W związku z tym mamy:

$\underset{-T/2}{\overset{T/2}{\int }}f(x)\cdot \cos n\omega x\text{d}x=a_n\frac{T}{2}$

Stąd otrzymujemy wzór Szablon:LinkWzór.

Dowód wzoru Szablon:LinkWzór przebiega analogicznie (tym razem mnożymy przez $\sin n\omega x$)

Twierdzenie (o rozwijalności funkcji w szereg Fouriera)

Jeżeli funkcja $f(x)$ jest różniczkowalna w punkcie $x_0,$ to jej szereg Fouriera jest zbieżny do wartości funkcji w tym punkcie.

Innymi słowy: W punktach różniczkowalności funkcję da się rozwinąć w szereg Fouriera.

Dowód

Niech $x_0$ będzie punktem, w którym funkcja $f(x)$ jest różniczkowalna; mamy:

$\begin{array}{cc}& a_n\cos n\omega x_0+b_n\sin n\omega x_0\\ =& \frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)\cos n\omega xdx\cos n\omega x_0+\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)\sin n\omega xdx\sin n\omega x_0\\ =& \frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)(\cos n\omega x\cos n\omega x_0+\sin n\omega x\sin n\omega x_0)dx\\ =& \frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)\cos n\omega (x-x_0)dx\end{array}$

Suma cząstkowa szeregu Fouriera przedstawia się w następujący sposób:

$\begin{array}{cc}{S}_N& =\frac{1}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)dx+\sum _{n=1}^N\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)\cos n\omega (x-x_0)dx\\ & =\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)(\frac{1}{2}+\sum _{n=1}^N\cos n\omega (x-x_0))dx\end{array}$

Stosując do tego wyrażenia lemat II, otrzymujemy następujący wzór:

$S_N=\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x)\frac{\sin \omega (N+\frac{1}{2})(x-x_0)}{2\sin \omega \frac{1}{2}(x-x_0)}dx$

Funkcja podcałkowa w powyższym wzorze jest funkcją o okresie T, możemy więc dokonać przesunięcia w dziedzinie i otrzymujemy:

$S_N=\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}f(x+x_0)\frac{\sin \omega (N+\frac{1}{2})x}{2\sin \omega \frac{1}{2}x}dx$

Funkcja tożsamościowo równa 1 na całym zbiorze liczb rzeczywistych jest rozwijalna w szereg Fouriera w każdym punkcie, kładąc $f(x)=1,$ mamy:

$1=\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}\frac{\sin \omega (N+\frac{1}{2})x}{2\sin \omega \frac{1}{2}x}dx$

Mnożąc powyższą równość przez $f(x_0)$ i odejmując obustronnie od równania przedstawiającego sumę cząstkową szeregu, otrzymujemy:Szablon:Wzór

Rozważmy następującą granicę:

$\underset{x\to 0}{\lim }\frac{f(x+x_0)-f(x_0)}{2\sin \omega \frac{1}{2}x}=\underset{x\to 0}{\lim }\frac{f(x+x_0)-f(x_0)}{x}\frac{x}{2\sin \omega \frac{1}{2}x}=\frac{f^{\prime }(x_0)}{\omega }$

przy obliczaniu której korzystamy z różniczkowalności funkcji f(x) w punkcie $x_0.$

Możemy określić następującą funkcję:

$\varphi (x)=\{\begin{array}{cccc}& \frac{f(x+x_0)-f(x_0)}{2\sin \omega \frac{1}{2}x}& & \text{gdy}x\ne 0\\ & \frac{f^{\prime }(x_0)}{\omega }& & \text{gdy}x=0\end{array}$

Mając na uwadze fakt, iż zmiana skończonej ilości wartości funkcji podcałkowej nie wpływa na wartość całki, wzór Szablon:LinkWzór możemy zapisać w postaci:

$S_N-f(x_0)=\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}\varphi (x)\sin \omega (N+\frac{1}{2})xdx$

Funkcja podcałkowa spełnia założenia lematu Riemanna, tak więc:

$\underset{N\to \mathrm{\infty }}{\lim }(S_N-f(x_0))=\underset{N\to \mathrm{\infty }}{\lim }\frac{2}{T}\underset{-T/2}{\overset{T/2}{\int }}\varphi (x)\sin \omega (N+\frac{1}{2})xdx=0$

czyli:

$\underset{N\to \mathrm{\infty }}{\lim }{S}_N=f(x_0).$

q. e. d.

Przestrzeń Hilberta a szereg Fouriera

Baza zespolona szeregu Fouriera

Uwaga: W poniższych rozważaniach przyjęto, iż szereg Fouriera jest funkcją o okresie $T=2\pi$. W przypadku $T\ne 2\pi$ wszystkie własności pozostają nadal prawdziwe, gdyż wystarczy przeskalować daną funkcję do funkcji o okresie $2\pi$.

Zbiór funkcji $\{e_n=e^{inx}:n\in \mathbb{Z}\}$ tworzy bazę ortonormalną przestrzeni funkcji całkowalnych w kwadracie $L^2([-\pi ,\pi ])$ na przedziale $[-\pi ,\pi ]$, w której iloczyn skalarny $⟨f|g⟩$ dwóch jej elementów $f$ oraz $g$ ma postać całkową:

$⟨f|g⟩=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)g^{*}(x)dx,$

gdzie $g^{*}(x)$ oznacza sprzężenie zespolone funkcji gdyż

$\underset{-\pi }{\overset{\pi }{\int }}{e}^{inx}\cdot e^{imx}dx=\{\begin{array}{cc}2\pi ,& \text{jeśli }n=-m\\ 0,& \text{jeśli }n\ne -m\end{array}$

Przestrzeń funkcyjna z tak zdefiniowanym iloczynem skalarnym jest nazywana przestrzenią Hilberta. Każdą funkcję $f$ tej przestrzeni można rozłożyć w jej bazie ortonormalnej w postaci szeregu

$f=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}⟨f|e_n⟩e_n$

Powyższy szereg przedstawia de facto szereg Fouriera funkcji $f$ w jego zespolonym sformułowaniu, gdzie zamiast funkcji bazowych $\sin (nx)$ oraz $\cos (nx)$ mamy funkcje zespolone $e_n=e^{inx}:n\in \mathbb{Z}$.

Baza ortogonalna z funkcji sin i cos szeregu Fouriera

Funkcje $f_m(x)=\sin (mx),$ $f_n(x)=\cos (nx),$$m,n\in N$ wraz z funkcją stałą $f_0(x)=1$ tworzą bazę ortogonalną przestrzeni Hilberta, gdyż: (1) całki z iloczynów $\sin (mx)\cdot \cos (nx)$zawsze są równe zero (obszary zielone i czerwone są równe i znoszą się), (2) całki z iloczynów $\sin (mx)\cdot \sin (nx)$ oraz $\cos (mx)\cdot \cos (nx)$ są niezerowe, równe $\pi$, tylko gdy $m=n$. Funkcje te tworzyłyby układ ortonormalny, gdyby całki te były równe 1, co można uzyskać mnożąc każdą funkcję sin i cos przez $1/\sqrt{\pi }$.

Jako bazę ortogonalną w przestrzeni funkcji całkowalnych w kwadracie $L^2([-\pi ,\pi ])$ na przedziale $[-\pi ,\pi ]$ można także wybrać funkcję stałą $f_0(x)=1$ oraz funkcje $\sin (mx),\cos (nx)$, dla $m,n=1,2,\dots$Analogicznie więc, jak dla bazy zespolonej, także szereg Fouriera z funkcjami sinus oraz cosinus przedstawia rozkład danej funkcji w bazie przestrzeni Hilberta.

Ortogonalność funkcji $\sin (nx)$ oraz $\cos (nx)$ wraz z funkcją stałą $f_0(x)=\cos (0x)=1$ wynika z poniższych całek:

$\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)\cos (nx)dx=\pi {\delta }_{mn},m,n\ge 1$$\underset{-\pi }{\overset{\pi }{\int }}\sin (mx)\sin (nx)dx=\pi {\delta }_{mn},m,n\ge 1$

$\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)\sin (nx)dx=0$

gdzie ${\delta }_{mn}=0$ gdy $m\ne n$, ${\delta }_{mn}=1$ gdy $m=n$ (tj. ${\delta }_{mn}$ oznacza symbol Kroneckera)

Tabela popularnych szeregów Fouriera

W tabeli zestawiono popularne funkcje okresowe i ich współczynniki szeregu Fouriera

• $s(x)$ oznacza funkcję okresową o okresie $P$
• $a_0,a_n,b_n$ oznaczają współczynniki szeregu Fouriera w formie trygonometrycznej (sin-cos) dla funkcji okresowych $s(x)$.

Funkcja oryginalna $s(x)$	Wykres funkcji	Współczynniki szeregu Fouriera w postaci trygonometrycznej $\begin{array}{cc}& a_0\\ & a_n\text{for }n\ge 1\\ & b_n\text{for }n\ge 1\end{array}$	Uwagi
$s(x)=A|\sin \left(\frac{2\pi }{P}x\right)|\text{dla }0\le x<P$		$\begin{array}{cc}{a}_0=& \frac{2A}{\pi }\\ a_n=& \{\begin{array}{cc}\frac{-4A}{\pi }\frac{1}{n^2-1}& n\text{ parzyste}\\ 0& n\text{ nieparzyste }\end{array}\\ b_n=& 0\\ \end{array}$	wartość bezwzględna funkcji sinus
$s(x)=\{\begin{array}{cc}A\sin \left(\frac{2\pi }{P}x\right)& \text{dla }0\le x<P/2\\ 0& \text{dla }P/2\le x<P\end{array}$		$\begin{array}{cc}{a}_0=& \frac{A}{\pi }\\ a_n=& \{\begin{array}{cc}\frac{-2A}{\pi }\frac{1}{n^2-1}& n\text{ parzyste}\\ 0& n\text{ nieparzyste}\end{array}\\ b_n=& \{\begin{array}{cc}\frac{A}{2}& n=1\\ 0& n>1\end{array}\\ \end{array}$	Funkcja sinus połówkowo filtrowana
$s(x)=\{\begin{array}{cc}A& \text{dla }0\le x<D\cdot P\\ 0& \text{dla }D\cdot P\le x<P\end{array}$		$\begin{array}{cc}{a}_0=& AD\\ a_n=& \frac{A}{n\pi }\sin \left(2\pi nD\right)\\ b_n=& \frac{2A}{n\pi }{(\sin \left(\pi nD\right))}^2\\ \end{array}$	$0\le D\le 1$
$s(x)=\frac{Ax}{P}\text{dla }0\le x<P$		$\begin{array}{cc}{a}_0=& \frac{A}{2}\\ a_n=& 0\\ b_n=& \frac{-A}{n\pi }\\ \end{array}$
$s(x)=A-\frac{Ax}{P}\text{dla }0\le x<P$		$\begin{array}{cc}{a}_0=& \frac{A}{2}\\ a_n=& 0\\ b_n=& \frac{A}{n\pi }\\ \end{array}$
$s(x)=\frac{4A}{P^2}{(x-\frac{P}{2})}^2\text{dla }0\le x<P$		$\begin{array}{cc}{a}_0=& \frac{A}{3}\\ a_n=& \frac{4A}{{\pi }^2{n}^2}\\ b_n=& 0\\ \end{array}$

Tabela podstawowych własności

Tabela zestawia operacje matematyczne wykonywane na danych funkcjach i wpływ tych operacji na współczynniki szeregów Fouriera oraz wpływ operacji wykonywanych na współczynnikach Fouriera i ich wpływ na dane funkcje. Notacja:

• Sprzężenie zespolone jest oznaczane gwiazdką.
• $s(x),r(x)$ oznaczają $T$-okresowe funkcje lub funkcje nieokresowe, zdefiniowane tylko dla $x\in [0,T].$
• $S[n],R[n]$ oznaczają współczynniki szeregów Fouriera w postaci zespolonej odpowiednio dla funkcji $s(x)$ oraz $r(x).$

Własności	Dziedzina funkcji	Dziedzina częstotliwości (dla postaci zespolonej szeregu)	Uwagi
Liniowość	$a\cdot s(x)+b\cdot r(x)$	$a\cdot S[n]+b\cdot R[n]$	$a,b\in ℂ$
Odwrócenie czasu / Odwrócenie częstotliwości	$s(-x)$	$S[-n]$
Sprzężenie w dziedzinie czasu	$s^{*}(x)$	$S^{*}[-n]$
Odwrócenie w dziedzinie czasu i sprzężenie	$s^{*}(-x)$	$S^{*}[n]$
Obliczanie części rzeczywistej funkcji	$\mathrm{Re}(s(x))$	$\frac{1}{2}(S[n]+S^{*}[-n])$
Obliczanie części urojonej funkcji	$\mathrm{Im}(s(x))$	$\frac{1}{2i}(S[n]-S^{*}[-n])$
Obliczanie części rzeczywistej współczynnika częstotliwości	$\frac{1}{2}(s(x)+s^{*}(-x))$	$\mathrm{Re}(S[n])$
Obliczanie części urojonej współczynnika częstotliwości	$\frac{1}{2i}(s(x)-s^{*}(-x))$	$\mathrm{Im}(S[n])$
Przesunięcie w czasie w danej funkcji / modulacja współczynników częstotliwości	$s(x-x_0)$	$S[n]\cdot e^{-i2\pi \frac{x_0}{P}n}$	$x_0\in ℝ$
Przesunięcie współczynników częstotliwości / modulacja danej funkcji	$s(x)\cdot e^{i2\pi \frac{n_0}{P}x}$	$S[n-n_0]$	$n_0\in \mathbb{Z}$

Szereg Fouriera funkcji 2 zmiennych

Szereg Fouriera dla funkcji dwóch zmiennych $x$ oraz $y$ określonych w dziedzinie $[-\pi ,\pi ]\times [-\pi ,\pi ]$ w formie zespolonej ma postać:

$f(x,y)=\sum _{m\in \mathbb{Z}}\sum _{n\in \mathbb{Z}}{c}_{mn}{e}^{imx}{e}^{iny},$

gdzie współczynniki rozwinięcia dane są wzorem

$c_{mn}=\frac{1}{4{\pi }^2}\underset{-\pi }{\overset{\pi }{\int }}\underset{-\pi }{\overset{\pi }{\int }}f(x,y)e^{-imx}{e}^{-iny}dxdy$

Bibliografia

• Szablon:Cytuj książkę
• Barbara Piłat, Mariusz. J. Wasilewski, Tablice całek, Wydawnictwo Naukowo-Techniczne, Warszawa 1985, s. 83-89 Współczynniki szeregów Fouriera wybranych funkcji. ISBN ISBN 978-83-20-40-525-5
• Tadeusz Trajdos, Matematyka dla inżynierów, PWN, Warszawa 1974, str. 534-544.
• Szablon:Cytuj książkę

Zobacz też

• transformata Fouriera
• dyskretna transformata Fouriera
• szybka transformata Fouriera

Inne:

• okno czasowe
• widmowa gęstość mocy

Linki zewnętrzne

Polskojęzyczne

• Szablon:Cytuj stronę

Anglojęzyczne

• Szablon:MathWorld
• Aplet Java obrazujący idee szeregu Fouriera
• Grant Sanderson, But what is a Fourier series? From heat flow to circle drawings, kanał 3blue1brown na YouTube, 30 czerwca 2019 [dostęp 2021-03-15].