Funkcja meromorficzna

Funkcja meromorficzna – funkcja $f,$ określona na otwartym podzbiorze $D$ płaszczyzny zespolonej, która jest funkcją holomorficzną w zbiorze $D\setminus S,$ gdzie $S$ oznacza zbiór punktów izolowanych, z których każdy jest biegunem funkcji $f$.

Termin ten pochodzi od greckiego meros (μέρος), oznaczającego „część”.

Przykłady

Funkcja Γ jako przykład funkcji meromorficznej

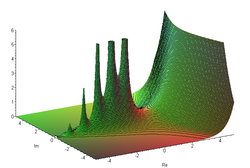
Funkcjami meromorficznymi są:

• wszystkie funkcje wymierne, np.

$f(z)=\frac{z^3-2z+1}{z^5+3z-1}$

Funkcja logarytmiczna $f(z)=\ln (z)$ nie jest funkcją meromorficzną - oś helisy stanowi punkt rozgałęzienia (pokazano tu wykres jej części urojonej).

• $f(z)=\frac{1}{\sin (z)}$ jest funkcją meromorficzną o nieskończenie wielu biegunach.
• $f(z)=\frac{{\mathrm{e}}^z}{z}$,
• $f(z)=\tan (z)$,
• $f(z)=\frac{\sin (z)}{(z-1{)}^2}$
• Funkcja Γ (gamma Eulera),
• funkcja ζ (dzeta Riemanna)

Funkcjami meromorficznymi nie są:

• wszystkie (niewymierne) funkcje algebraiczne (np.$\sqrt{z}$)
• funkcja logarytmiczna $f(z)=\ln (z)$
• dowolna funkcja mająca punkt rozgałęzienia
• $f(z)={\mathrm{e}}^{\frac{1}{z}}$ oraz każda funkcja posiadająca zasadniczą osobliwość gdzie indziej niż w nieskończoności
• wszystkie funkcje posiadające kumulację osobliwości (np.: punkt generujący szereg podziałów ).

Twierdzenia I

• Każda funkcja holomorficzna jest meromorficzna.
• Funkcje wymierne, w szczególności homograficzne, są funkcjami meromorficznymi.
• Każda funkcja meromorficzna na płaszczyźnie domkniętej (tzn. na Sfera Riemanna ), jest funkcją wymierną.
• Funkcje eliptyczne są „dwuokresowymi” funkcjami meromorficznymi określonymi na $ℂ.$
• Funkcje modularne, czyli funkcje meromorficzne określone na górnej półpłaszczyźnie hiperbolicznej, są niezmiennicze na działanie grupy modularnej; w szczególności istnieje tzw. niezmiennik j.

Twierdzenia II

Tw. 1 Każdą funkcję meromorficzną na sferze Riemanna można wyrazić za pomocą ilorazu dwóch funkcji holomorficznych:

$f(z)=\frac{h_1(z)}{h_2(z)},$

przy czym funkcja $h_2$ nie może być stale równa $0.$ Zbiór biegunów $S$ jest zbiorem zer funkcji $h_2.$

Tw. 2 Jeżeli zbiór $D$ jest spójny, to zbiór wszystkich określonych na nim funkcji meromorficznych tworzy ciało (które można utożsamiać z ciałem ułamków pierścienia funkcji holomorficznych w $D$).

Tw. 3 Funkcje meromorficzne można utożsamiać z odwzorowaniami powierzchni Riemanna

$f:D\to {\mathbb{P}}_1,$

gdzie ${\mathbb{P}}_1$ oznacza sferę Riemanna, nazywana okresem funkcji $\mathrm{\infty }.$

Zobacz też

• biegun (analiza zespolona)

Bibliografia

• Szablon:Cytuj książkę

Linki zewnętrzne

• Funkcje meromorficzne na MathWorld