Biegun (analiza zespolona)

Bieguny funkcji Gamma

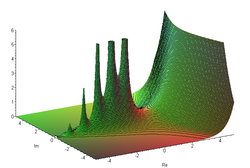
Biegun funkcji meromorficznej $f(z)$ – taki punkt osobliwy $z=a$ funkcji meromorficznej, w którego otoczeniu funkcja ta nie jest ograniczona, zaś w punkcie $z=a$ przyjmuje wartość nieskończoną, tj.

$\lim {\mathrm{\backslash limits}}_{z\to a}f(z)=+\mathrm{\infty }$ lub $\lim {\mathrm{\backslash limits}}_{z\to a}f(z)=-\mathrm{\infty }$

Ponadto: a). jeśli część osobliwa rozwinięcia w szereg Laurenta wokół punktu $z=a$ składa się z $k<\mathrm{\infty }$ wyrazów, to biegun ten jest rzędu $k$ b). jeśli $k=\mathrm{\infty }$, to punkt $z=a$ jest punktem istotnie osobliwym, tzn. nie istnieje granica $\lim {\mathrm{\backslash limits}}_{z\to a}f(z)$

Uwaga: Brak granicy występuje, gdy funkcja $f(z)$ przyjmuje różne wartości przy zbliżaniu się do punktu osobliwego. Jedną z możliwości jest rozbieżność analogiczna jak funkcji rzeczywistych, gdzie istnieją różne granice lewo- i prawostronna; np. funkcja $f(x)=\frac{1}{x}$ nie ma granicy w punkcie x=0, gdyż$\lim {\mathrm{\backslash limits}}_{x\to 0^{-}}\frac{1}{x}=-\mathrm{\infty }$ , zaś $\lim {\mathrm{\backslash limits}}_{x\to 0^{+}}\frac{1}{x}=+\mathrm{\infty }$

Twierdzenia o biegunach i zerach funkcji f oraz 1/f

Tw. 1 Jeśli punkt a jest biegunem $m$-krotnym funkcji $f(z)$, to funkcja $g(z)=\frac{1}{f(z)}$ jest również meromorficzna i w punkcie $z=a$ posiada zero $m$-krotne. Odwrotnie, jeśli punkt $z=a$ jest zerem $m$-krotnym funkcji$f(z)$, to funkcja w tym punkcie posiada biegun $m$-krotny.

Tw. 2 Jeśli punkt $z=a$ jest biegunem $m$-krotnym funkcji $f(z)$ to funkcja $g(z)$ jest również meromorficzna i w punkcie $z=a$ posiada zero $m$-krotne.

Przykłady

Przykład 1: Funkcja $f(z)=\mathrm{tg}(z)$

w punktach $z=\pi (k-\frac{1}{2})$ ma bieguny rzędu 1.

Przykład 2: Funkcja

$f(z)=\frac{1}{2-z}+\frac{1}{(z-1{)}^2}$

a) Bieguny: w punkcie $z=1$ ma biegun rzędu 2, natomiast w punkcie $z=2$ ma biegun jednokrotny.

b) Zera: Aby obliczyć zera tej funkcji, sprowadzamy ułamki do wspólnego mianownika; po przekształceniach otrzymamy:

$f(z)=\frac{z^2-3z+3}{(2-z)(z-1{)}^2}$

Rozwiązując równanie kwadratowe, występujące w liczniku, otrzymamy

$f(z)=\frac{(z-z_1)(z-z_2)}{(2-z)(z-1{)}^2}$

gdzie:

$z_1=\frac{3+\sqrt{3}i}{2}$, $z_2=\frac{3-\sqrt{3}i}{2}$ - zera funkcji $f(z)$

c) Funkcja odwrócona: Postać funkcji $g(z)=\frac{1}{f(z)}$ łatwo znaleźć zamieniając miejscami licznik i mianownik funkcji $f(z)$

$g(z)=\frac{(2-z)(z-1{)}^2}{(z-z_1)(z-z_2)}$

Stąd widać, że funkcja $g(z)$ ma zera tam, gdzie funkcja $f(z)$ ma bieguny i odwrotnie - tam, gdzie funkcja $f(z)$ ma bieguny, tam funkcja $f(z)$ ma zera. Krotności zer i odpowiadających im biegunów obu funkcji są identyczne.

Bibliografia

• W. Żakowski, W. Leksiński, Matematyka cz. IV, Wydawnictwo Naukowo-Techniczne, Warszawa 1978, Rozdział III Funkcje zmiennej zespolonej, s. 233-350. ISBN 978-83-01-19359-1