Wahadło sferyczne

Wahadło sferyczne, kąty i prędkości

Wahadło sferyczne – punktowa masa zawieszona na nierozciągliwej nici zamocowanej w punkcie. Swobodę ruchu wahadła ogranicza tylko nić.

Wahadło sferyczne ma położenie równowagi, w którym nić wahadła jest pionowa.

Wahadło takie w ogólności porusza się po elipsie wykreślonej na powierzchni sfery ograniczającej ruch wahadła.

Historia

Pierwsze systematyczne prace nad badaniem ruchu wahadła sferycznego prowadził w drugiej połowie XVII wieku Christiaan Huygens. W swej pracy dotyczącej konstrukcji dokładnego zegara z wahadłem stożkowym wymienia kilkanaście związków między prędkością, promieniem, okresem ruchu wahadła stożkowego i ich znaczenie w praktycznej konstrukcji zegara.

W publikacji z 1735 roku Alexis Clairaut znajduje wyrażenia na małą zmianę położenia wahadła. Zapisuje wyrażenia całkowe na ruch wahadła sferycznego i wskazuje, że nie można ich rozwiązać analitycznie. Zapisuje wyrażenia na najmniejszą i największą wysokość wahadła w zależności od jego położenia i prędkości początkowej. Znajduje zależność czasu wahnięcia od wysokości maksymalnej wahadła. Rozwiązuje niektóre szczególne przypadki ruchu wahadła.

Postęp w analizie wahadła wnosi nowy formalizm analizy ruchu prowadzony przez Lagrange’a w 1788 roku. Choć nie zachowały się publikacje Lagranga opisujące rozwiązania wahadła, to autorzy podręczników z XIX w odsyłają do jego prac.

W XIX wahadło sferyczne nie wzbudzało większego zainteresowania. Było tylko kilka krótkich prac na jego temat. Jedną z nich były praca Puiseux z 1842 roku, w której autor koncentruje się na własnościach orbity, a nie na szukaniu pełnego rozwiązania. Udowadnia matematycznie, obserwowane własności orbity. Bez względu na parametry początkowe ruchu minimalna wysokość wahadła jest poniżej punktu zawieszenia (kąt większy od 90°). W płaszczyźnie poziomej ruchu wahadła opisuje elipsa, której osie obracają się (precesja) w tym samym kierunku w którym obciążnik obiega elipsę. W 1851 roku George Biddell Airy formułuje wzór na precesję wahadła, wykonuje eksperymenty z ruchem wahadła.

Richelot wydaje pracę, w której rozważa wahadło w przybliżeniu małych drgań jako równania i rozpatruje zaburzenia jego ruchu w wyniku wzrostu amplitudy, oporów.

Prawdopodobnie jako pierwszy w 1852 roku Tissot wprowadza nową teorię całek funkcji eliptycznych do opisu wahadła sferycznego.

Przybliżenie małego kąta wychyleń

Dla małych kątów wychyleń można przyjąć, że $sin\theta =\theta ,$ wówczas równania ruchu można opisać w kartezjańskim układzie współrzędnych:

$m\frac{d^{2}x}{d{t}^2}=-\frac{mg}{l}x,$

$m\frac{d^{2}y}{d{t}^2}=-\frac{mg}{l}y.$

Rozwiązania można zapisać jako:

$x(t)=A\cos (\omega t+{\varphi }_x),$

$y(t)=B\cos (\omega t+{\varphi }_y),$

gdzie:

${\omega }^2=\frac{g}{l}.$

W tym przybliżeniu wahadło takie bez względu na warunki początkowe wykonuje drgania z częstotliwością taką samą jak wahadło matematyczne.

Stałe ruchu A_x, A_y, ${\varphi }_x,{\varphi }_y$ określa się na podstawie warunków początkowych ruchu wahadłaSzablon:R. Przyjmując, że w chwili $t=0$ wahadło znajduje się w punkcie nawrotu (x <> 0, y = 0, Vx <> 0 i Vy = 0), to równania ruchu można zapisać:

$x(t)=A\cos (\omega t),$

$y(t)=B\sin (\omega t).$

Są to równania parametryczne elipsy o półosiach A i B. Wahadło porusza się po elipsie bez zmiany płaszczyzny osi elipsy.

Opis matematyczny

Współrzędne wahadła

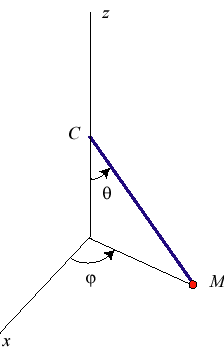
Położenie wahadła można opisać w kartezjańskim układzie współrzędnych lub w sferycznym o początku w punkcie zawieszenia wahadła. Oś z jest pionowa.

Związki między współrzędnymi:

$x=l\sin \theta \cos \varphi ,$

$y=l\sin \theta \sin \varphi ,$

$z=l\cos \theta .$

Energia potencjalna i kinetyczna wahadła:

$E_p=mgz=-mgl\cos \theta ,$

$E_k=\frac{m{v}^2}{2}=\frac{1}{2}m{l}^2({\dot{\theta }}^2+{\sin }^2\theta {\dot{\varphi }}^2).$

Lagranżjan dla tego układu wynosi:

$L=\frac{1}{2}m{l}^2({\dot{\theta }}^2+si{n}^2\theta {\dot{\varphi }}^2)+mgl\cos \theta .$

Pochodna względem szybkości zmiany kąta θ jest momentem pędu wahadła względem osi z i jest stała:

$M_z=\frac{\partial L}{\partial \dot{\theta }}=m{l}^{2}si{n}^2\theta \dot{\varphi }.$

Równanie ruchu wahadła:

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0.$

Z równania ruchu wynika:

$\ddot{\theta }+\frac{g}{l}\sin \theta -\sin \theta \cos \theta {\dot{\varphi }}^2=0.$

W ogólności równania nie można rozwiązać metodami analitycznymi.

Wahadło proste

Jeżeli φ jest stałe, wówczas jego pochodna jest równa 0, skutkuje tym, że trzeci wyraz jest równy 0, wówczas równanie sprowadza się do równania wahadła matematycznego.

$\ddot{\theta }+\frac{g}{l}\sin \theta =0.$

Wahadło takie porusza się w płaszczyźnie.

Wahadło stożkowe

Jeżeli wahadło nie zmienia swej odległości od punktu równowagi (θ jest stała), równanie sprowadza się do:

$\frac{g}{l}=\cos \theta {\dot{\varphi }}^2.$

Co prowadzi do wyrażeń na częstość i okres wahadła:

$\omega =\dot{\varphi }=\sqrt{\frac{g}{l\cos \theta }}=\frac{{\omega }_0}{\sqrt{\cos \theta }}.$

Wahadło porusza się po poziomym okręgu, a powyższe równanie określa prędkość kątową ciała w tym ruchu. Promień okręgu wynosi:

$R=l\cos \theta .$

Dla małych promieni częstość, a tym samym i okres drgań, jest taki jak dla wahadła prostego. W miarę wzrostu częstości rośnie wychylenie.

Precesja

Tor ruchu wahadła sferycznego.

Przyjmując, że wahadło sferyczne jest zaburzonym wahadłem stożkowym, wprowadzając oznaczenie

$\theta ={\theta }_0+\partial \theta ,$

gdzie:

${\theta }_0$ – częstość wahadła stożkowego.

Po rozłożeniu równania wahadła w szereg Taylora i pozostawiając jedynie wyrazy pierwszego stopnia, w przybliżeniu:

$\partial \ddot{\theta }+{\dot{\varphi }}_0^2(1+3co{s}^2{\theta }_0)\partial \theta \approx 0.$

Rozwiązaniem tego równania jest:

$\theta \approx {\theta }_0+\partial {\theta }_0\cos (\mathrm{\Omega }t),$

gdzie:

$\mathrm{\Omega }={\dot{\varphi }}_0\sqrt{1+3{\cos }^2{\theta }_0}.$

Zatem kąt $\theta$ wykonuje prosty ruch harmoniczny o średniej wartości ${\theta }_0,$ zmieniając się z częstością kątową $\mathrm{\Omega }.$

Teraz kąt $\varphi$ jest zwiększony o

$\mathrm{\Delta }\varphi \approx {\dot{\varphi }}_0\frac{\pi }{\mathrm{\Omega }}=\frac{\pi }{\sqrt{1+3{\cos }^2{\theta }_0}}.$

Kąt nachylenia względem pionowej, $\theta ,$ przechodzi pomiędzy kolejnymi maksimami i minimami. Jeżeli, ${\theta }_0$ jest mały, to $\mathrm{\Delta }\varphi$ jest nieco większa niż $\pi /2.$ Skoro, $\mathrm{\Delta }\varphi$ jest nieco większa niż $\pi /2$ (90°) oznacza, że kształt ten precesuje wokół osi z w tym samym kierunku co obrót wahadła. Precesja wzrasta gdy kąt nachylenia ${\theta }_0$ wzrasta.

Dla wahadła poruszającego się prawie w płaszczyźnie, precesję określa przybliżony wzór na prędkość kątową obrotu osi elipsy (precesja Airy):

${\omega }_{pr}=\frac{3A}{4l^{2}T}=\frac{3}{8}\frac{ab}{l^2}{\omega }_w=\frac{3}{8}\frac{ab}{g^2}{\omega }_w^5,$

gdzie:

$a,b$ – półosie elipsy,

$g$ – przyspieszenie ziemskie,

${\omega }_w$ – częstość kołowa wahadła.

Zobacz też

• wahadło Foucaulta