Twierdzenie Carathéodory’ego (teoria miary)

Szablon:Spis treści Twierdzenie Carathéodory’ego – twierdzenie teorii miary umożliwiające konstrukcję miary w oparciu o daną miarę zewnętrzną; bywa ono stosowane do konstrukcji miary Lebesgue’a z miary zewnętrznej Lebesgue’a. Twierdzenie to zostało udowodnione przez Constantina Carathéodory’ego w 1914 roku.

Twierdzenie

Niech $X$ będzie niepustym zbiorem oraz

${\mu }^{*}:P(X)\to [0,\mathrm{\infty }]$

będzie funkcją, dla której

${\mu }^{*}(\varnothing )=0,$

gdzie $P(X)$ oznacza zbiór potęgowy zbioru $X.$

Mówi się, że zbiór $A\subseteq X$ spełnia warunek Carathéodory’ego (względem ${\mu }^{*}$), gdy dla każdego zbioru $E\subseteq X$ zachodzi równość

${\mu }^{*}(E)={\mu }^{*}(E\cap A)+{\mu }^{*}(E\cap A^{\mathrm{c}}).$

Wówczas rodzina $C({\mu }^{*})$ podzbiorów $X,$ które spełniają warunek Carathéodory’ego względem ${\mu }^{*},$ jest algebrą zbiorów, a $\mu$ będąca zawężeniem ${\mu }^{*}$ do $C({\mu }^{*})$ jest miarą skończenie addytywną (tzn. jest addytywna). Co więcej, jeśli ${\mu }^{*}$ jest miarą zewnętrzną (tzn. jest również monotoniczna i przeliczalnie podaddytywna), to $C({\mu }^{*})$ jest σ-algebrą oraz ${\mu }^{*}$ zawężona do rodziny $C({\mu }^{*})$ jest miarą (tzn. jest przeliczalnie addytywna), która jest zupełna.

Dowód

Dowód składa się z pięciu części. Wykorzystuje on standardowe techniki, szeroko stosowane w teorii miary. Pierwsze dwa kroki mają na celu wykazanie, iż $C({\mu }^{*})$ jest algebrą, zaś $\mu$ jest addytywna; trzeci i czwarty gwarantują – przy założeniu, iż ${\mu }^{*}$ jest miarą zewnętrzną – że rodzina $C({\mu }^{*})$ jest zamknięta ze względu na sumy przeliczalnie wielu zbiorów, a ${\mu }^{*}$ jest σ-addytywna, tzn. $C({\mu }^{*})$ jest σ-algebrą, a $\mu$ określoną na niej miarą. W ostatnim kroku dowodzi się zupełności miary $\mu .$

Algebra

Należenie zbioru pustego

Zbiór pusty spełnia warunek Carathéodory’ego, ponieważ z założenia ${\mu }^{*}(\varnothing )=0$ oraz

${\mu }^{*}(E\cap \varnothing )+{\mu }^{*}(E\cap X)={\mu }^{*}(\varnothing )+{\mu }^{*}(E)={\mu }^{*}(E)$

dla każdego $E$ zawartego w $X.$

Zamkniętość ze względu na dopełnienia

Warunek Carathéodory’ego jest niezmienniczy względem brania dopełnienia, tzn. jeśli $A$ spełnia warunek Carathéodory’ego, to spełnia go również $A^c.$

Zamkniętość ze względu na sumy skończone

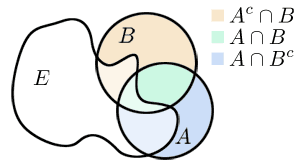
Niech $A$ oraz $B$ należą do $C({\mu }^{*})$ oraz $E$ będzie dowolnym podzbiorem $X.$ Zachodzą równości

${\mu }^{*}(E)={\mu }^{*}(E\cap A)+{\mu }^{*}(E\cap A^{\mathrm{c}})$

oraz

${\mu }^{*}(E)={\mu }^{*}(E\cap A)+{\mu }^{*}(E\cap A^{\mathrm{c}}\cap B)+{\mu }^{*}(E\cap A^{\mathrm{c}}\cap B^{\mathrm{c}}).$

Z tożsamości $E\cap A=E\cap (A\cup B)\cap A$ oraz $E\cap A^c\cap B=E\cap (A\cup B)\cap A^c$ oraz założenia, że $A$ spełnia warunek Carathéodory’ego wynika, iż

${\mu }^{*}(E\cap (A\cup B))={\mu }^{*}(E\cap A)+{\mu }^{*}(E\cap A^{\mathrm{c}}\cap B),$

skąd

${\mu }^{*}(E)={\mu }^{*}(E\cap (A\cup B))+{\mu }^{*}(E\cap A^{\mathrm{c}}\cap B^{\mathrm{c}})={\mu }^{*}(E\cap (A\cup B))+{\mu }^{*}(E\cap (A\cup B{)}^{\mathrm{c}}).$

Dowodzi to, że $A\cup B$ spełnia warunek Carathéodory’ego, a zatem należy do $C({\mu }^{*}).$

Addytywność zawężenia

Dla danych zbiorów rozłącznych $A$ i $B$ należących do $C({\mu }^{*})$ zachodzi równość

${\mu }^{*}(A\cup B)={\mu }^{*}((A\cup B)\cap A)+{\mu }^{*}((A\cup B)\cap A^{\mathrm{c}})={\mu }^{*}(A)+{\mu }^{*}(B).$

Pokazuje to, że zawężenie ${\mu }^{*}$ do rodziny $C({\mu }^{*})$ jest addytywną funkcją zbiorów.

σ-algebra

Niżej zakłada się, że ${\mu }^{*}$ jest miarą zewnętrzną.

Niech $(C_i)$ będzie przeliczalną rodziną zbiorów należących do $C({\mu }^{*})$ oraz niech $E$ będzie dowolnym podzbiorem zbioru $X.$ Utwórzmy przeliczalne rodziny $(A_i),$ $(B_i)$ następująco:

$A_1=C_1,C_n=A_n\setminus \left(\bigcup _{i=1}^{n-1}{A}_i\right)\text{dla }n=2,3,4,\dots$

$B_n=\bigcup _{i=1}^n{A}_i,$

oraz wprowadźmy oznaczenie

$B:=\bigcup _{i=1}^{\mathrm{\infty }}{A}_i.$

Zbiory $A_n$ są parami rozłączne i zachodzi oczywista równość

$B=\bigcup _{i=1}^{\mathrm{\infty }}{C}_i.$

Dla każdego $n$ zachodzi inkluzja $B_n\subseteq B,$ skąd $B_n^c\supseteq B^c.$ Korzystając z monotoniczności ${\mu }^{*},$ otrzymujemy oszacowanie

${\mu }^{*}(E)={\mu }^{*}(E\cap B_n)+{\mu }^{*}(E\cap B_n^{\mathrm{c}})⩾{\mu }^{*}(E\cap B_n)+{\mu }^{*}(E\cap B^{\mathrm{c}}).$

Z faktu, że każdy zbiór $A_n$ spełnia warunek Carathéodory’ego, wnioskujemy, że dla $n⩾2$ prawdziwa jest tożsamość

${\mu }^{*}(E\cap B_n)={\mu }^{*}(E\cap A_n)+{\mu }^{*}(E\cap B_{n-1}).$

Na mocy zasady indukcji matematycznej, równość

${\mu }^{*}(E\cap B_n)=\sum _{i=1}^n{\mu }^{*}(E\cap A_i)$

zachodzi dla wszystkich $n\in \mathbb{N}.$ Ostatecznie,

${\mu }^{*}(E)⩾\sum _{i=1}^n{\mu }^{*}(E\cap A_i)+{\mu }^{*}(E\cap B^{\mathrm{c}})(n\in \mathbb{N}).$

Wykonując przejście graniczne, otrzymujemy oszacowanie

${\mu }^{*}(E)⩾\sum _{i=1}^{\mathrm{\infty }}{\mu }^{*}(E\cap A_i)+{\mu }^{*}(E\cap B^{\mathrm{c}}).$

Z przeliczalnej podaddytywności ${\mu }^{*}$ wynika nierówność

$\sum _{i=1}^{\mathrm{\infty }}{\mu }^{*}(E\cap A_i)⩾{\mu }^{*}(\bigcup _{i=1}^{\mathrm{\infty }}(E\cap A_i))={\mu }^{*}(E\cap B).$

Łącząc otrzymane związki i korzystając ponownie z przeliczalnej podaddytywności ${\mu }^{*},$ uzyskujemy zależność

${\mu }^{*}(E)⩾{\mu }^{*}(E\cap B)+{\mu }^{*}(E\cap B^{\mathrm{c}})⩾{\mu }^{*}((E\cap B)\cup (E\cap B^{\mathrm{c}}))={\mu }^{*}(E).$

Miara

Niżej zakłada się, że ${\mu }^{*}$ jest miarą zewnętrzną.

Niech $(A_i)$ będzie przeliczalną rodziną parami rozłącznych zbiorów należących do $C({\mu }^{*}).$ Niech ponadto $B$ będzie sumą wszystkich zbiorów $A_i.$ Z addytywności i monotoniczności ${\mu }^{*}$ wynika, że dla dowolnego $n$ zachodzi równość

${\mu }^{*}(A_1)+\dots +{\mu }^{*}(A_n)={\mu }^{*}(A_1\cup \dots \cup A_n)⩽{\mu }^{*}(B).$

Wykonując przejście graniczne, otrzymujemy oszacowanie

$\sum _{i=1}^{\mathrm{\infty }}{\mu }^{*}(A_i)⩽{\mu }^{*}(B).$

Przeliczalna podaddytywność ${\mu }^{*}$ daje nierówność w drugą stronę.

Zupełność

Niżej zakłada się, że ${\mu }^{*}$ jest miarą zewnętrzną.

Należy wykazać, że każdy podzbiór $A$ zbioru $X$ spełniający warunek ${\mu }^{*}(A)=0$ należy do $C({\mu }^{*}).$ Niech $E$ będzie dowolnym podzbiorem zbioru $X.$ Wówczas

${\mu }^{*}(E)={\mu }^{*}((E\cap A)\cup (E\cap A^{\mathrm{c}}))⩽{\mu }^{*}(E\cap A)+{\mu }^{*}(E\cap A^{\mathrm{c}})⩽{\mu }^{*}(A)+{\mu }^{*}(E)={\mu }^{*}(E).$

Niech $Z$ będzie podzbiorem zbioru $X$ spełniającym warunek ${\mu }^{*}(Z)=0$ oraz niech $A$ będzie dowolnym podzbiorem zbioru $Z.$ Z monotoniczności ${\mu }^{*}$ wynika, że $0⩽{\mu }^{*}(A)⩽{\mu }^{*}(Z)=0,$ a więc ${\mu }^{*}(A)=0.$ Ostatecznie, $A$ należy do rodziny $C({\mu }^{*}).$

Zobacz też

• twierdzenie Hahna-Kołmogorowa

Bibliografia

• Szablon:Cytuj książkę
• Szablon:Cytuj książkę
• Szablon:Cytuj książkę
• Szablon:Cytuj książkę
• Szablon:Cytuj książkę
• Szablon:Cytuj książkę