Hiperboloida

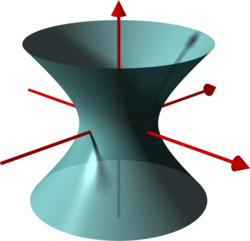Hiperboloida jednopowłokowa

powierzchnia stożkowa pomiędzy

Hiperboloida dwupowłokowa

Hiperboloidowa wieża ciśnień w Ciechanowie

Hiperboloida – nieograniczona, nierozwijalna powierzchnia drugiego stopnia (kwadryka), powstała przez obrót hiperboli wokół osi symetrii hiperboli rozłącznej z nią (hiperboloida jednopowłokowa) lub osi prostopadłej do poprzedniej, przechodzącej przez oba wierzchołki hiperboli (hiperboloida dwupowłokowa), a także każda otrzymana z takiej przez przekształcenie afiniczne przestrzeni. Każda hiperboloida ma środek symetrii oraz co najmniej trzy osie i trzy płaszczyzny symetrii.

Równania hiperboloidy

Można ją opisać wzorem

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$  (hiperboloida jednopowłokowa)

lub

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1$  (hiperboloida dwupowłokowa).

Równanie hiperboloidy można sparametryzować poprzez funkcję $f:{ℝ}^2\to {ℝ}^3$ daną wzorem:

$f(s,t)=(a\sqrt{s^2+1}\cos t,b\sqrt{s^2+1}\sin t,cs)$ (dla hiperboloidy jednopowłokowej)

lub

$f(s,t)=(a\sqrt{s^2-1}\cos t,b\sqrt{s^2-1}\sin t,cs)$ (dla hiperboloidy dwupowłokowej).

Obie hiperboloidy są asymptotyczne do powierzchni stożka o równaniu

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0.$

Szczególne przypadki

Hiperboloidę obrotową otrzymuje się tylko gdy $a^2=b^2.$ W przeciwnym razie osie symetrii są jednoznacznie określone (z dokładnością do zamiany osi x z osią y).

Hiperboloida jednopowłokowa zwana też hiperboloidą hiperboliczną ma ujemną krzywiznę Gaussa w każdym punkcie. Implikuje to, że każda powierzchnia styczna do niej zawiera dwie proste, leżące w hiperboloidzie – hiperboloida ta jest więc powierzchnią prostokreślną.

Hiperboloida dwupowłokowa zwana hiperboloidą eliptyczną ma dodatnią krzywiznę Gaussa w każdym punkcie. Dlatego jest powierzchnią wypukłą w tym sensie, że powierzchnia styczna w każdym punkcie przecina tę powierzchnię tylko w punkcie styczności.

Zastosowanie kształtu

W XIX wieku kształt hiperboloidy obrotowej nadawano panoramom malarskim dla spotęgowania efektu zacierania się granicy między powierzchnią płótna a przestrzenią przed nim. Jednym z przykładów takiego zastosowania jest Panorama Racławicka. Także koła zębate przekładni hipoidalnych mają kształt hiperboloidy dwupowłokowej, a jej nazwa prawdopodobnie powstała ze skrótu: hiperboloidalna > hipoidalna.

Linki zewnętrzne

• Szablon:Cytuj stronę Szablon:Lang
• Szablon:MathWorld