Epitrochoida

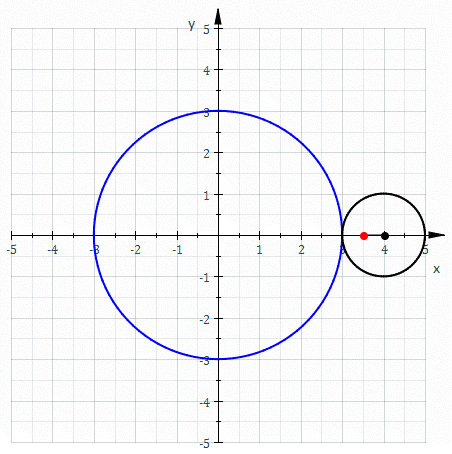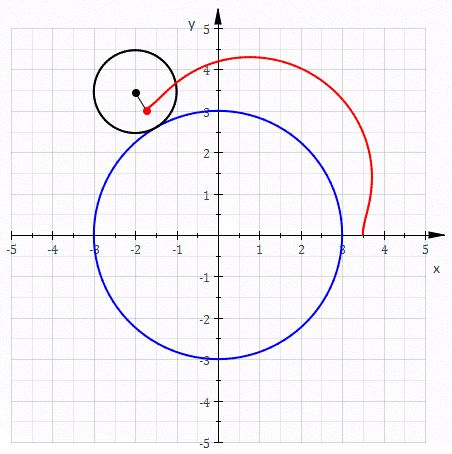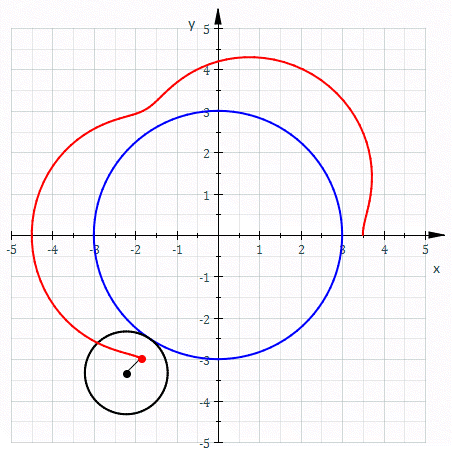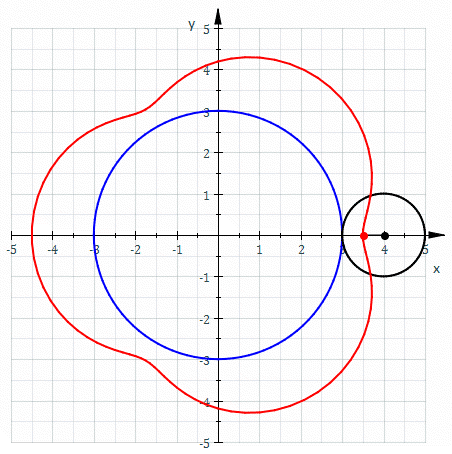
Epitrochoida – krzywa zakreślona przez punkt pozostający w stałym położeniu względem koła toczącego się po pewnym nieruchomym okręgu.

Epitrochoidę najłatwiej opisać równaniami parametrycznymi:

x = (R + r) \cos t - h \cos (\frac{R + r}{r} t),

y = (R + r) \sin t - h \sin (\frac{R + r}{r} t),

gdzie:

R

– promień nieruchomego okręgu,

r

– promień toczącego się koła,

h

– odległość punktu od środka koła o promieniu

r .

Wzajemna zależność promienia $r$ koła i odległości $h$ punktu opisującego krzywą od środka tego koła, pozwala na otrzymanie:

Jeżeli stosunek $\frac{R}{r}$ jest liczbą niewymierną, otrzymuje się krzywą otwartą.

Ciekawym zastosowaniem praktycznym epitrochoidy w technice jest cylinder silnika Wankla.

Zobacz też