Twierdzenie Cevy (trygonometryczne)

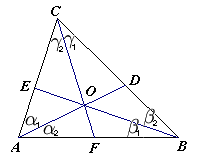
Wersja trygonometryczna twierdzenia Cevy pozwala na pokazanie, że proste Cevy w trójkącie przecinają się w jednym punkcie, gdy mamy pewne dane o kątach, ale nie mamy danych o tym, w jakim stosunku te proste dzielą boki trójkąta.

Treść

Jeżeli proste Cevy $AD,$ $BE,$ $CF$ w trójkącie $ABC$ przecinają się w jednym punkcie, to przy oznaczeniach kątów jak na rysunku zachodzi równość:

$\sin {\alpha }_1\cdot \sin {\beta }_1\cdot \sin {\gamma }_1=\sin {\alpha }_2\cdot \sin {\beta }_2\cdot \sin {\gamma }_2.$

Dowód

Z twierdzenia Cevy mamy:

$\frac{|AF|}{|FB|}\cdot \frac{|BD|}{|DC|}\cdot \frac{|CE|}{|EA|}=1.$

Z twierdzenia sinusów mamy:

$\frac{|AF|}{|AC|}=\frac{\sin {\gamma }_2}{\sin \mathrm{\angle }AFC}$

oraz

$\frac{|FB|}{|BC|}=\frac{\sin {\gamma }_1}{\sin \mathrm{\angle }BFC},$

$\sin \mathrm{\angle }BFC=\sin \mathrm{\angle }AFC,$ (kąty przyległe),

więc

$\frac{|AF|}{|FB|}=\frac{\sin {\gamma }_2}{\sin {\gamma }_1}\cdot \frac{AC}{BC}.$

Podobnie

$\frac{|BD|}{|DC|}=\frac{\sin {\alpha }_2}{\sin {\alpha }_1}\cdot \frac{AB}{AC},$

$\frac{|CE|}{|EA|}=\frac{\sin {\beta }_2}{\sin {\beta }_1}\cdot \frac{BC}{AB}.$

Mnożąc stronami, dostajemy

$1=\frac{|AF|}{|FB|}\cdot \frac{|BD|}{|DC|}\cdot \frac{|CE|}{|EA|}=\frac{\sin {\gamma }_2}{\sin {\gamma }_1}\cdot \frac{\sin {\alpha }_2}{\sin {\alpha }_1}\cdot \frac{\sin {\beta }_2}{\sin {\beta }_1}.$

Twierdzenie odwrotne

Jeżeli proste Cevy spełniają przy oznaczeniach jak na rysunku

$\sin {\alpha }_1\cdot \sin {\beta }_1\cdot \sin {\gamma }_1=\sin {\alpha }_2\cdot \sin {\beta }_2\cdot \sin {\gamma }_2,$

to przecinają się w jednym punkcie.

Dowód

Dowód prowadzimy korzystając z twierdzenia odwrotnego do twierdzenia Cevy i analogicznie za pomocą zależności

$\frac{|AF|}{|FB|}=\frac{\sin {\gamma }_2}{\sin {\gamma }_1}\cdot \frac{AC}{BC},$

$\frac{|BD|}{|DC|}=\frac{\sin {\alpha }_2}{\sin {\alpha }_1}\cdot \frac{AB}{AC},$

$\frac{|AF|}{|FB|}=\frac{\sin {\beta }_2}{\sin {\beta }_1}\cdot \frac{BC}{AB},$

sprowadzamy równość

$\frac{|AF|}{|FB|}\cdot \frac{|BD|}{|DC|}\cdot \frac{|CE|}{|EA|}=1$

do postaci trygonometrycznej

$1=\frac{\sin {\gamma }_2}{\sin {\gamma }_1}\cdot \frac{\sin {\alpha }_2}{\sin {\alpha }_1}\cdot \frac{\sin {\beta }_2}{\sin {\beta }_1}.$

Zastosowania

Za pomocą twierdzenia można łatwo udowodnić, że w każdym trójkącie w jednym punkcie przecinają się dwusieczne, symediany, wysokości, środkowe. Nie znaczy to jednak, że punkty przecięcia np. wysokości i symetralnych są tym samym punktem. Taki przypadek występuje tylko w trójkącie równobocznym.

Zobacz też

• twierdzenie Cevy