Pentagramma mirificum

Przykładowe konfiguracje pentagramma mirificum

Zależności między kątami i bokami pięciu trójkątów prostokątnych przyległych do wewnętrznego pięciokąta: ich koła Nepera zawierają przesunięte cyklicznie części $(a,$ $\pi /2-B,$ $\pi /2-c,$ $\pi /2-A,$ $b)$

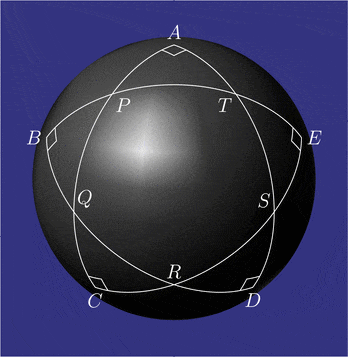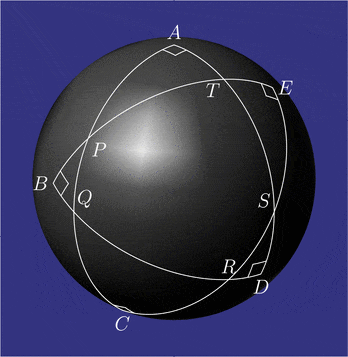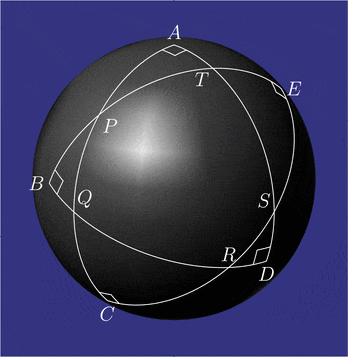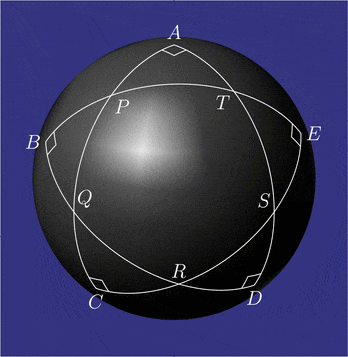
Pentagramma mirificum (łac. cudowny pentagram) – w geometrii sferycznej wielokąt gwiaździsty złożony z pięciu łuków kół wielkich, którego wszystkie kąty wewnętrzne są proste. Figurę tę opisał John Napier w pracy Mirifici Logarithmorum Canonis Descriptio (Opis cudownej tabeli logarytmów) z roku 1614 wraz z regułą Nepera, która wiąże wartości funkcji trygonometrycznych pięciu części trójkąta sferycznego prostokątnego (dwóch kątów i trzech boków). Własności pentagramma mirificum badał między innymi Carl Friedrich Gauss.

Własności geometryczne

Na sferze miarą kąta wyraża się zarówno kąty, jak i boki trójkątów sferycznych (łuki kół wielkich). Kąty $A,$ $B,$ $C,$ $D$ i $E$ są proste. Miara łuków $PC,$ $PE,$ $QD,$ $QA,$ $RE,$ $RB,$ $SA,$ $SC,$ $TB$ i $TD$ wynosi $\pi /2.$ W pięciokącie sferycznym $PQRST$ każdy wierzchołek jest biegunem przeciwległego boku. Na przykład punkt $P$ jest biegunem równika $RS,$ punkt $Q$ – biegunem równika $ST$ i tak dalej. Miara kąta zewnętrznego przy każdym wierzchołku pięciokąta $PQRST$ jest równa mierze przeciwległego boku. Na przykład $\mathrm{\angle }APT=\mathrm{\angle }BPQ=\stackrel{⌢}{RS},$ $\mathrm{\angle }BQP=\mathrm{\angle }CQR=\stackrel{⌢}{ST}$ i tak dalej. Koła Nepera trójkątów $APT,$ $BQP,$ $CRQ,$ $DSR$ i $ETS$ są obrócone względem siebie.

Wzory Gaussa

Gauss wprowadził oznaczenia Szablon:Wzór

Zachodzą następujące tożsamości, które pozwalają na wyznaczenie dowolnych trzech z powyższych wielkości na podstawie dwóch pozostałych:

$1+\alpha =\gamma \delta ,$

$1+\beta =\delta ϵ,$

$1+\gamma =ϵ\alpha ,$

$1+\delta =\alpha \beta ,$

$1+ϵ=\beta \gamma .$

Gauss udowodnił następującą „piękną równość” (schöne Gleichung): Szablon:Wzór

Spełniają ją na przykład liczby $(\alpha ,\beta ,\gamma ,\delta ,\epsilon )=(9,2/3,2,5,1/3),$ których iloczyn $\alpha \beta \gamma \delta \epsilon$ wynosi $20.$

Dowód pierwszej części równości:

$\alpha \beta \gamma \delta \epsilon$ $=\alpha \beta \gamma \left(\frac{1+\alpha }{\gamma }\right)\left(\frac{1+\gamma }{\alpha }\right)$ $=\beta +\alpha \beta +\beta \gamma +\alpha \beta \gamma$ $=\beta +1+\delta +1+\epsilon +\alpha (1+\epsilon )$ $=2+\alpha +\beta +\delta +\epsilon +1+\gamma$ $=3+\alpha +\beta +\gamma +\delta +\epsilon$ c.b.d.u.

Dowód drugiej części równości:

$\sqrt{(1+\alpha )(1+\beta )(1+\gamma )(1+\delta )(1+\epsilon )}$ $=\sqrt{{}^{{}^{{}^{}}}\alpha \beta \cdot \beta \gamma \cdot \gamma \delta \cdot \delta \epsilon \cdot \epsilon \alpha }$ $=\sqrt{{\alpha }^2{\beta }^2{\gamma }^2{\delta }^2{\epsilon }^2}$ $=\alpha \beta \gamma \delta \epsilon$ c.b.d.u.

Również od Gaussa pochodzi wzór Szablon:Wzór gdzie $S_{PQRST}=2\pi -(|\stackrel{⌢}{PQ}|+|\stackrel{⌢}{QR}|+|\stackrel{⌢}{RS}|+|\stackrel{⌢}{ST}|+|\stackrel{⌢}{TP}|)$ to pole powierzchni pięciokąta $PQRST.$

Rzut gnomoniczny

Obrazem pięciokąta sferycznego $PQRST$ w rzucie gnomonicznym (rzucie o środku w środku sfery) na dowolną płaszczyznę styczną do sfery jest pięciokąt prostoliniowy. Jak wiadomo, przez jego pięć wierzchołków $P^{\prime }{Q}^{\prime }{R}^{\prime }{S}^{\prime }{T}^{\prime }$ przechodzi dokładnie jedna krzywa stożkowa; w tym wypadku jest to elipsa. Gauss wykazał, że wysokości pięciokąta $P^{\prime }{Q}^{\prime }{R}^{\prime }{S}^{\prime }{T}^{\prime }$ (proste przechodzące przez wierzchołki i prostopadłe do przeciwległych boków) przecinają się w jednym punkcie $O^{\prime },$ który jest obrazem punktu styczności płaszczyzny rzutu i sfery.

Arthur Cayley zauważył, że jeśli obrać środek układu współrzędnych kartezjańskich w punkcie $O^{\prime },$ to między współrzędnymi wierzchołków $P^{\prime }{Q}^{\prime }{R}^{\prime }{S}^{\prime }{T}^{\prime }:$ $(x_1,y_1),\dots ,(x_5,y_5)$ zachodzi związek $x_1{x}_4+y_1{y}_4$ $=x_2{x}_5+y_2{y}_5$ $=x_3{x}_1+y_3{y}_1$ $=x_4{x}_2+y_4{y}_2$ $=x_5{x}_3+y_5{y}_3=-{\varrho }^2,$ gdzie $\varrho$ to długość promienia sfery.

Linki zewnętrzne

• Szablon:YouTube