Hipocykloida

Hipocykloida – krzywa płaska, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu wewnątrz okręgu o większym promieniu. Krzywa ta jest szczególnym przypadkiem hipotrochoidy.

Kształt hipocykloidy (liczba ostrzy) zależy od ilorazu $\frac{R}{r}$ promieni okręgów, nieruchomego do toczącego się.

Opis matematyczny

Hipocykloidę najłatwiej opisać równaniami parametrycznymi:

$x=(R-r)\cos (t)+r\cos \left(\frac{R-r}{r}t\right),$

$y=(R-r)\sin (t)-r\sin \left(\frac{R-r}{r}t\right).$

Przykłady

Asteroida jako ewoluta elipsy

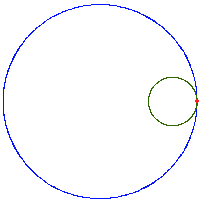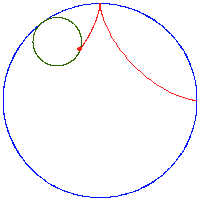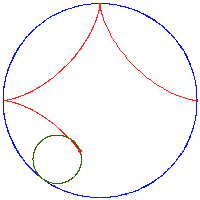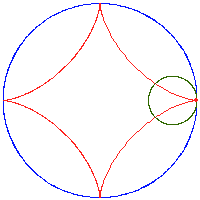
Poniższe rysunki pokazują kilka hipocykloid dla różnych wartości ilorazów $\frac{R}{r}$

• hipocykloida $\frac{R}{r}=3$ (zwana też deltoidą) – powstawanie i krzywa statycznie:

• hipocykloida $\frac{R}{r}=4$ (zwana też asteroidą) – powstawanie i krzywa statycznie:

• dla $\frac{R}{r}=2$ hipocykloida redukuje się do średnicy dużego okręgu – fakt ten jest znany jako twierdzenie Kopernika i może być wykorzystany do zamiany ruchu obrotowego na posuwisto-zwrotny:

Jeżeli stosunek $\frac{R}{r}$ jest liczbą niewymierną, hipocykloida jest linią otwartą, a zbiór jej wierzchołków jest gęstym podzbiorem okręgu. Poniższe rysunki przedstawiają taką sytuację z tym, że parametr $t$ przebiega skończony przedział, [−10, 100] oraz [−10, 1000]:

Zobacz też

• cykloida
• epicykloida
• lista krzywych

Linki zewnętrzne

• Szablon:MathWorld