Paraboloida hiperboliczna: Różnice pomiędzy wersjami
Przejdź do nawigacji
Przejdź do wyszukiwania
imported>Tarnoob →Linki zewnętrzne: szablon |
(Brak różnic)
|
Aktualna wersja na dzień 21:49, 1 wrz 2023

[−5,5]x[−5,5]
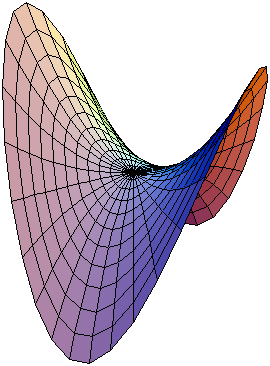
Paraboloida hiperboliczna – nieograniczona powierzchnia drugiego stopnia posiadająca jedną oś symetrii i dwie płaszczyzny symetrii, jedna z dwóch odmian paraboloidy obok paraboloidy eliptycznej.
Powierzchnia ta powstaje w wyniku przesunięcia paraboli wzdłuż innej paraboli, przy czym obydwie parabole muszą spełniać następujące warunki[1]:
- muszą się znajdować w płaszczyznach prostopadłych do siebie,
- ich osie symetrii muszą być równoległe,
- ich ramiona muszą być skierowane w przeciwne strony.
Równanie

Paraboloida hiperboliczna, niezależnie od jej ustawienia w przestrzeni i doboru układu współrzędnych, spełnia równanie powierzchni drugiego stopnia[2]:
przy czym w celu odróżnienia jej od innych takich powierzchni należy zastosować warunki:
oraz
Odpowiednio dobierając układ współrzędnych, można jej równanie zapisać w postaci[1]:
lub