Liczby Armstronga
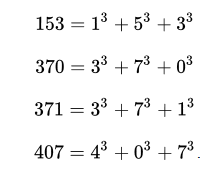
Liczba Armstronga (narcystyczna) – n-cyfrowa liczba naturalna, która jest sumą swoich cyfr podniesionych do potęgi
Definicja
Niech będzie liczbą naturalną z reprezentacją w systemie o podstawie (tak więc dla ). Jeśli dla pewnej liczby naturalnej zachodzi
to powiemy, że jest m-narcystyczną liczbą w bazie .
Liczba narcystyczna to n-cyfrowa n-narcystyczna liczba w bazie dziesiętnej. Tak więc liczby narcystyczne to n-cyfrowe liczby naturalne spełniające warunek:
gdzie: to kolejne cyfry liczby (od najbardziej znaczącej do najmniej znaczącej).
Własności
- Istnieją dokładnie cztery liczby 3-narcystyczne:
- Istnieją dokładnie trzy liczby 4-narcystyczne:
- Istnieją dokładnie trzy liczby 5-narcystyczne:
- Istnieje dokładnie jedna liczba 6-narcystyczna:
- Istnieją dokładnie cztery liczby 7-narcystyczne:
- Jeśli jest liczbą narcystyczną, to
Ponieważ dla to z powyższych nierówności wnioskujemy, że istnieje skończona liczba liczb Armstronga. Pokazano, że istnieje dokładnie 88 takich liczb. Największa z nich to 115132219018763992565095597973971522401, składająca się z 39 cyfr.
Linki zewnętrzne
- Szablon:MathWorld [dostęp 2022-07-02].
Szablon:Teoria liczb Szablon:Typy liczb naturalnych Szablon:Szablon nawigacyjny