Drzewo pitagorejskie

Drzewo Pitagorasa

Pokolorowany fraktal ze zmienionymi długościami przyprostokątnych

Ilustracja do twierdzenia Pitagorasa, od którego fraktal wziął swoją nazwę

Drzewo pitagorejskie (także drzewo Pitagorasa) – fraktal zbudowany z kwadratów na płaszczyźnie, swym kształtem przypominający drzewo. Nazwany został od imienia greckiego matematyka i myśliciela Pitagorasa, gdyż na każdym etapie konstrukcji wymaga rysowania dwóch kwadratów opartych na odpowiednich bokach trójkąta prostokątnego, których własności stanowią ilustrację twierdzenia Pitagorasa. Rozważane są drzewa symetryczne, w konstrukcji których występują trójkąty prostokątne równoramienne, i drzewa ogólne, w konstrukcji których występują trójkąty prostokątne z kątami ostrymi ustalonymi, ale innymi niż 45°.

Pierwszy rysunek fraktala został sporządzony (ręcznie) w roku 1942 przez holenderskiego inżyniera i nauczyciela matematyki Alberta E. Bosmana (1891–1961). Bosman opisał fraktal i jego własności w roku 1957 w swoim dziele Het wondere onderzoekingsveld der vlakke meetkunde.

Odpowiednio użyty, może służyć do przedstawiania informacji w postaci struktury danych drzewa. Jest też bardzo łatwy w wykonaniu.

Podczas Festiwalu Symetrii w Delfcie w Holandii w 2013 roku (The 2013 Symmetry Festival), pokazano drzewo pitagorejskie zbudowane z drewnianych prostopadłościanów, które ułożone były przy pomocy trójkątów prostokątnych równoramiennych.

Konstrukcja

1. Konstrukcja fraktala zaczyna się od narysowania dowolnego kwadratu.
2. Dorysowujemy do niego trójkąt prostokątny, w którym przeciwprostokątna jest górną krawędzią tego kwadratu.
3. Na przyprostokątnych trójkąta budujemy kolejne kwadraty.
4. Powtarzamy powyższe operacje 2 i 3.

Poniżej przedstawione zostały kolejne iteracje. Możliwa jest też zmiana długości przyprostokątnych tak, że wyższe „gałęzie” zmienią kierunek, w którym powstają.

Kolejne etapy konstrukcji fraktala

• 
• 
• 
• 

Właściwości i wygląd

Drzewo Pitagorejskie można narysować tylko w przybliżeniu, gdyż pełny fraktal składa się z nieskończonej liczby coraz mniejszych trójkątów i kwadratów.

Pole powierzchni

Uwaga: Ta sekcja dotyczy konstrukcji wykorzystującej trójkąt prostokątny równoramienny.

Zakładając, że początkowy kwadrat jest jednostkowy, $n$-ta iteracja w konstrukcji „dodaje” $2^n$ kwadratów o długości boku ${\left(\frac{\sqrt{2}}{2}\right)}^n$ każdy. Niektóre kwadraty mogą na siebie nachodzić. Jeśli początkowy kwadrat ma wymiary $a\times a,$ to całe drzewo zmieści się w prostokącie o wymiarach $6a\times 4a$.

Dowód

Wysokość prostokąta, w którym zmieści się fraktal

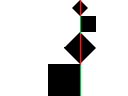
Szablon:Clear Niech początkowy kwadrat będzie jednostkowy, a kolejne trójkąty prostokątne równoramienne. Dodajmy teraz do siebie długości boków kwadratów oraz długości przekątnych kwadratów, jak na ilustracji powyżej. W rezultacie tej operacji otrzymamy sumę dwóch szeregów szeregów geometrycznych. Zatem wysokość $H$ drzewa Pitagorasa wynosi:

$\begin{array}{cc}H& =1+\sqrt{2}\cdot \left(\frac{\sqrt{2}}{2}\right)+{\left(\frac{\sqrt{2}}{2}\right)}^2+\sqrt{2}\cdot {\left(\frac{\sqrt{2}}{2}\right)}^3+{\left(\frac{\sqrt{2}}{2}\right)}^4+\sqrt{2}\cdot {\left(\frac{\sqrt{2}}{2}\right)}^5+\dots \\ & =(1+\sqrt{2}\cdot \left(\frac{\sqrt{2}}{2}\right))\cdot \sum _{n=1}^{\mathrm{\infty }}{\left(\frac{\sqrt{2}}{2}\right)}^{n-1}\\ & =(1+\sqrt{2}\cdot \left(\frac{\sqrt{2}}{2}\right))\cdot \frac{1}{1-\frac{1}{2}}=4.\end{array}$

Szerokość prostokąta, w którym zmieści się fraktal

Szablon:Clear Niech początkowy kwadrat ma długość boku $1,$ a kolejne trójkąty niech będą prostokątne i równoramienne. Weźmy pod uwagę jedynie kwadraty umieszczone najniżej na pierwszej „gałęzi” fraktala odchodzącej w prawo lub w lewo.

Korzystając z symetrii, chcemy obliczyć tylko szerokość kwadratów przechodzących w prawo. Nie uwzględniamy początkowego kwadratu. Sumujemy odpowiednie długości przekątnych kwadratów i długości boków kwadratów. Zatem szerokość $W$ połowy fraktala wyrażamy wzorem:

$\begin{array}{cc}W& =\sqrt{2}\cdot \left(\frac{\sqrt{2}}{2}\right)+{\left(\frac{\sqrt{2}}{2}\right)}^2+\sqrt{2}\cdot {\left(\frac{\sqrt{2}}{2}\right)}^3+{\left(\frac{\sqrt{2}}{2}\right)}^4+\sqrt{2}\cdot {\left(\frac{\sqrt{2}}{2}\right)}^5+\dots \\ & =(\sqrt{2}\cdot \left(\frac{\sqrt{2}}{2}\right)+{\left(\frac{\sqrt{2}}{2}\right)}^2)\cdot \sum _{n=1}^{\mathrm{\infty }}{\left(\frac{\sqrt{2}}{2}\right)}^{n-1}\\ & =\frac{3}{2}\cdot \sum _{n=1}^{\mathrm{\infty }}{\left(\frac{\sqrt{2}}{2}\right)}^{n-1}\\ & =\frac{3}{2}\cdot \frac{1}{1-\frac{1}{2}}=3.\end{array}$

Zatem szerokość całego fraktala jest równa $6.$

Drzewo pitagorejskie a notacja binarna

Specjalną właściwością fraktala jest możliwość znajdywania konkretnych kwadratów po przypisaniu im liczb określoną metodą.

Oznaczmy początkowy kwadrat numerem 1. Dla dowolnej liczby naturalnej $n,$ nad kwadratem o numerze $n,$ skonstruowanym dwóm kwadratom przypiszemy numery $2n$ i $2n+1.$

Jeżeli kwadraty zostaną oznakowane w powyższy sposób, możemy użyć dwójkowego systemu liczbowego, by znaleźć konkretny kwadrat.

Zapiszmy liczby w systemie dziesiętnym systemem dwójkowym. Niech 1 odpowiada skrętowi w prawo (do prawego kwadratu), a zero w lewo (do lewego sąsiadującego kwadratu).

Przykład:

• 45 = 101101_2, z czego wynika, że by dostać się do kwadratu oznaczonego numerem 45, musimy skręcić w prawo, w lewo, dwa razy w prawo, w lewo i w prawo.

Pokrewieństwo z innymi fraktalami

Jeśli początkowy trójkąt fraktala będzie prostokątny i równoramienny, to po kilkunastu iteracjach „korona” drzewa będzie krzywą Lévy’ego.

Wybierając kwadraty o indeksach (zdefiniowanych tak jak w sekcji powyżej) stanowiących potęgi liczby dwa uzyskamy spiralę logarytmiczną; działa to jednak także z dowolnie wybranym kwadratem, pod warunkiem, że kolejne będą zawsze kwadratami po jego prawej lub lewej stronie. Liczba możliwych do utworzenia w ten sposób spiral jest więc nieskończona.

Wykorzystanie

Pokolorowane drzewo Pitagorasa

Fraktal wykorzystywany jest jako prosta wizualizacja działania twierdzenia Pitagorasa. Jest prosty do stworzenia np. na lekcji matematyki. Wykorzystuje się go także do produkcji anten fraktalnych oraz do wizualizacji informacji w postaci struktury danych drzewa.

Bibliografia

• Het wondere onderzoekingsveld der vlakke meetkunde
• Szablon:MathWorld

Linki zewnętrzne

• Generator drzewa Pitagorasa
• Generowanie fraktala w różnych językach programowania