Pseudookrąg

Pseudookrąg – przykład, o znaczeniu teoretycznym, spełniającej aksjomat $T_0$, czteropunktowej skończonej przestrzeni topologicznej. Jest to najmniejsza, w sensie liczby punktów, przestrzeń topologiczna mająca nieskończoną grupę podstawową.

Definicja

Pseudookrąg jest przestrzenią topologiczną określoną na zbiorze ${𝒮}^1=\{a,b,c,d\}$, w której topologią jest rodzina $$\{{𝒮}^1,\{a,b,c\},\{a,c,d\},\{a,c\},\{a\},\{c\},\varnothing \}.$$

Topologia ta, podobnie jak topologia każdej $T_0$-przestrzeni Aleksandrowa, odpowiada pewnemu częściowemu porządkowi, który można przedstawić na poniższym diagramie Hassego

.

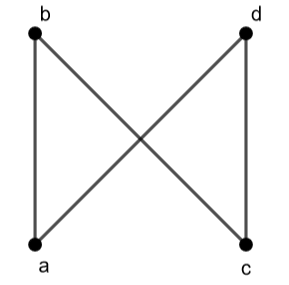
Bazą tej topologii są zbiory 'zniżkowe' względem wspomnianego uporządkowania, tj. zbiory postaci $$U_x=\{y\in {𝒮}^1:y⩽x\}$$ dla $x\in {𝒮}^1$.

Własności

• ${𝒮}^1$ jest $T_0$-przestrzenią Aleksandrowa, lecz nie jest przestrzenią $T_1$.
• Pseudookrąg jest słabo homotopijnie równoważny ze sferą ${𝕊}^1$ (tj. okręgiem ze standardową topologią). Z tego wynika, że obie przestrzenie mają izomorficzne grupy homotopii oraz homologii. W szczególności, grupa podstawowa ${\pi }_1({𝒮}^1)$ jest izomorficzna z grupą liczb całkowitych $\mathbb{Z}$.
• Pseudookrąg nie jest homotopijnie równoważny sferze ${𝕊}^1$.

Zobacz też

• Skończona przestrzeń topologiczna
• Przestrzeń Aleksandrowa