Przyspieszenie

Szablon:Dopracować Szablon:Wielkość fizyczna infobox Przyspieszenie – wektorowa wielkość fizyczna wyrażająca zmianę wektora prędkości w czasie.

Przyspieszenie definiuje się jako pochodną prędkości po czasie, czyli jest szybkością zmiany prędkości. Jeśli przyspieszenie jest skierowane przeciwnie do zwrotu prędkości ruchu, to wartość prędkości w tym ruchu maleje, a przyspieszenie to jest wtedy nazywane opóźnieniem.

Definicja

Definicja przyspieszenia

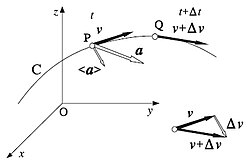
Jeżeli dany wektor $\overrightarrow{r}$ określa położenie punktu materialnego, a wektor $\overrightarrow{v}$ określa prędkość tego punktu, to jego przyspieszenie $\overrightarrow{a}$ jest pochodną prędkości po czasie:

$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}.$

Ponieważ prędkość z kolei jest pochodną położenia po czasie, to przyspieszenie można zapisać jako drugą pochodną położenia po czasie:

$\overrightarrow{a}=\frac{d^2\overrightarrow{r}}{d{t}^2}.$

Jednostką przyspieszenia w układzie SI jest metr na sekundę do kwadratu.

$[\overrightarrow{a}]=\frac{m}{s^2}.$

Związek z dynamiką

Zgodnie z drugą zasadą dynamiki przyspieszenie $\overrightarrow{a}$ ciała jest proporcjonalne do wypadkowej siły $\overrightarrow{F}$ działającej na to ciało i odwrotnie proporcjonalne do masy ciała $m.$ Kierunek i zwrot przyspieszenia $\overrightarrow{a}$ pokrywa się z kierunkiem i zwrotem siły $\overrightarrow{F}.$ Wzór wyrażający tę zależność ma postać

$\overrightarrow{a}=\frac{\overrightarrow{F}}{m}.$

W ruchu prostoliniowym

W ruchu po linii prostej kierunek prędkości jest ustalony, więc można ją traktować tak jak wielkość skalarną. Wówczas przyspieszenie określa wzór:

$a=\frac{dv}{dt}.$

W ruchu jednostajnie zmiennym

Gdy przyspieszenie jest stałe ($a=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$), wzór definicyjny przybiera postać

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t},$

gdzie $\mathrm{\Delta }v$ jest przyrostem prędkości w czasie $\mathrm{\Delta }t.$

Przyspieszenie w ruchu krzywoliniowym

Przyspieszenie styczne $a_t$ i normalne $a_n$

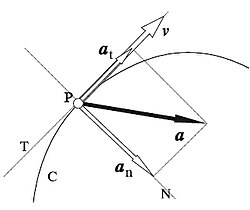
Jeżeli punkt porusza się po torze krzywoliniowym, wówczas jego całkowite przyspieszenie może być rozłożone na dwie składowe: prostopadłą do toru ruchu zwaną przyspieszeniem dośrodkowym lub normalnym (oznaczanym ${\overrightarrow{a}}_n$) i składową równoległą do toru, zwaną przyspieszeniem stycznym (ozn. ${\overrightarrow{a}}_t$).

Wektor $\overrightarrow{a}$ przyspieszenia całkowitego jest sumą jego składowych – normalnej ${\overrightarrow{a}}_n$ i stycznej ${\overrightarrow{a}}_t:$

$\overrightarrow{a}={\overrightarrow{a}}_n+{\overrightarrow{a}}_t.$

Składowe – styczna i normalna – są wzajemnie prostopadłe i dlatego wartość przyspieszenia całkowitego jest równa:

$|\overrightarrow{a}|=\sqrt{|{\overrightarrow{a}}_n{|}^2+|{\overrightarrow{a}}_t{|}^2}.$

Przyspieszenie dośrodkowe (normalne)

Szablon:Osobny artykuł Jest to składowa przyspieszenia prostopadła do toru ruchu. Reprezentuje tę część przyspieszenia, która wpływa na zmianę kierunku prędkości, a zatem na kształt toru, ale nie wpływa na zmianę wartości prędkości. Jeżeli prędkość chwilowa oznaczona jest jako $v,$ a chwilowy promień zakrzywienia toru (promień okręgu stycznego do toru, czyli promień krzywizny toru) ruchu wynosi $r,$ to wartość $a_n$ przyspieszenia dośrodkowego ciała jest równa:

$a_n=\frac{v^2}{r}.$

Przyspieszenie styczne

Jest to składowa przyspieszenia styczna do toru ruchu, powodująca zmianę wartości prędkości, ale nie powodująca zmiany kierunku ruchu. Stosując oznaczenie $v$ dla wartości prędkości chwilowej i oznaczenie $s$ dla drogi pokonanej przez ciało, przyspieszenie styczne $a_t$ określają wzory:

$a_t=\frac{dv}{dt}=\frac{d^{2}s}{d{t}^2}.$

Przyspieszenie kątowe

Przyspieszenie kątowe ciała jest wielkością opisującą jego ruch obrotowy, utworzoną analogicznie do przyspieszenia liniowego, tylko wyrażoną w wielkościach kątowych. Jest pseudowektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt $\alpha ,$ a $\omega$ oznacza jego prędkość kątową, to wartość przyspieszenia kątowego $\epsilon$ określa wzór

$\epsilon =\frac{d\omega }{dt}=\frac{d^2\alpha }{d{t}^2}[\epsilon ]=\frac{1}{{\text{s}}^2}.$

Jednostką przyspieszenia kątowego w układzie SI jest jeden radian przez sekundę do kwadratu.

Dowolne współrzędne krzywoliniowe

Niech współrzędne krzywoliniowe $q_1(t),q_2(t),q_3(t)$ tworzą układ współrzędnych w przestrzeni $R^3.$ Oznaczmy przez ${𝐞}_1,{𝐞}_2,{𝐞}_3$ wersory kierunków stycznych do osi tego układuSzablon:R.

Jeżeli $𝐚$ jest wektorem przyspieszenia, to jego rzuty na osie układu współrzędnych można zapisać wzorami Szablon:Wzór

Ponieważ

$\frac{d}{dt}(𝐯{𝐞}_i)=\dot{𝐯}{𝐞}_i+𝐯\frac{d}{dt}{𝐞}_i⟶\dot{𝐯}{𝐞}_i=\frac{d}{dt}(𝐯{𝐞}_i)-𝐯\frac{d}{dt}{𝐞}_i$

zatem Szablon:Wzór

Na podstawie wzoru dla prędkości Szablon:Wzór

mamy Szablon:Wzór

i dzięki temu Szablon:Wzór

Mamy również Szablon:Wzór

oraz Szablon:Wzór

Z porównania prawych stron Szablon:LinkWzór i Szablon:LinkWzór wynika, że Szablon:Wzór

Mamy zatem Szablon:Wzór

Po podstawieniu Szablon:LinkWzór i Szablon:LinkWzór do Szablon:LinkWzór otrzymujemy następujące wzory dla rzutów $a_i$ wektora przyspieszenia $𝐚$ na osie krzywoliniowego układu współrzędnych Szablon:Wzór

Pomiar

Do pomiaru służy przetwornik przyspieszenia nazywany przyspieszeniomierzem lub akceleromierzem czy akcelerometrem.

Zobacz też

• grawitacja
• przyspieszenie grawitacyjne
• przyspieszenie ziemskie