Pryzmat

Widmo światła białego (dziennego), uzyskane za pomocą pryzmatu szklanego równobocznego

Rozszczepienie światła białego w pryzmacie o dużej i małej dyspersji

Pryzmat rozszczepiający światło

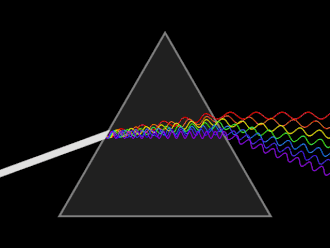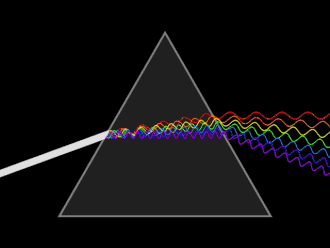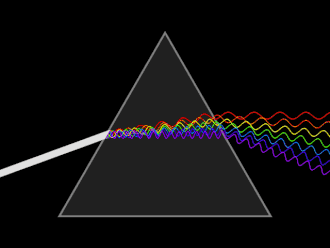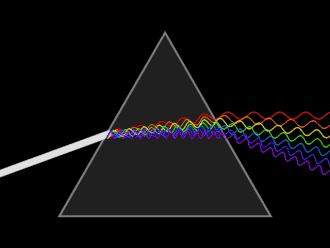
Pryzmat – bryła z materiału przezroczystego o co najmniej dwóch ścianach płaskich nachylonych do siebie pod kątem $\omega$ (tzw. kątem łamiącym pryzmatu).

Używany w optyce do zmiany kierunku biegu fal świetlnych, a poprzez to, że zmiana kierunku zależy od długości fali, jest używany do analizy widmowej światła. Zjawisko całkowitego wewnętrznego odbicia pozwala użyć pryzmatu jako elementu odbijającego światło.

Pryzmaty wykorzystywane są w produkcji wielu urządzeń optycznych, np.: lornetek, peryskopów.

Dający najszerszą tęczę pryzmat wykonany ze szkła kwarcowego ma kąt $\omega$ między ścianami wynoszący 62°, ze szkła crown ZN – 78°, a ze szkła flint – ok. 82°–86°Szablon:Fakt.

Szczególne rodzaje pryzmatów:

• pryzmat pentagonalny
• pryzmat Nicola
• pryzmat Wollastona

Kąt załamania w pryzmacie

Bieg promienia świetlnego przez pryzmat.

Kąt odchylenia promienia i dyspersji przez pryzmat można określić za pomocą prawa Snelliusa na powierzchniach pryzmatu.

$\begin{array}{cc}{\beta }_1& =\arcsin (\frac{n_0}{n_1}\sin {\alpha }_1)\\ {\beta }_2& =\omega -{\beta }_1\\ {\alpha }_2& =\arcsin (\frac{n_1}{n_2}\sin {\beta }_2)\end{array}$

Dla pryzmatu, którego obie powierzchnie stykają się z tą samą substancją oba współczynniki załamania są takie same, wprowadza się wówczas względny współczynnik załamania ośrodków n, kąt załamania promienia $\delta$ jest określony przez:

$\begin{array}{cc}\delta & ={\alpha }_1+{\alpha }_2-\omega \\ & ={\alpha }_1+\arcsin (n\sin [\omega -\arcsin (\frac{1}{n}\sin {\alpha }_1)])-\omega .\end{array}$

Jeśli kąt padania promienia na pryzmat ${\alpha }_1$ i kąt wyjścia promienia z pryzmatu ${\alpha }_2$ są niewielkie, to powyższy wzór można przybliżyć wzorem:

$\delta \approx {\alpha }_1-\omega +n\left[(\omega -\frac{1}{n}{\alpha }_1)\right]=(n-1)\omega ,$

gdzie:

${\alpha }_1$ – kąt padania promienia padającego na pryzmat,

${\beta }_2$ – kąt padania promienia wychodzącego z pryzmatu,

${\beta }_1$ – kąt załamania promienia padającego na pryzmat,

${\alpha }_2$ – kąt załamania promienia wychodzącego z pryzmatu,

$n_0,$ $n_1,$ $n_2$ – współczynnik załamania kolejnych ośrodków przez które biegnie promień.

Minimalny kąt załamania pryzmatu

Promień, przechodząc przez pryzmat, ulega najmniejszemu odchyleniu, gdy kąt padania promienia na pryzmat jest równy kątowi wyjścia promienia z pryzmatu. Wówczas:

$n\sin \frac{\omega }{2}=\sin \frac{\omega +\delta }{2},$

$\delta =2\arcsin (n\sin \frac{\omega }{2})-\omega .$

Zjawisko to ma wpływ na zjawiska optyczne w atmosferze takie jak halo i tęcza. Gdy promień świetlny, przechodząc przez kryształu lodu, przechodzi przez ścianki nachylone do siebie pod kątem 60°, to minimalne odchylenie promienia jest równe 22° i odpowiada za tworzenie się halo 22°. Gdy promień przechodzi przez ścianki prostopadłe do siebie, to minimalny kąt odchylenia jest równy 46° i odpowiada za tworzenie się halo 46°.

Kąt graniczny całkowitego wewnętrznego odbicia

Całkowite wewnętrzne odbicie w pryzmacie

Jeżeli kąt padania promienia świetlnego wychodzącego z pryzmatu na płaszczyznę jest większy od kąta granicznego, to promień nie wychodzi z pryzmatu a ulega całkowitemu wewnętrznemu odbiciu. Sytuacja ta zachodzi gdy:

$\sin {\alpha }_{gr}=n\sin (\omega -\arcsin \frac{1}{n})$

lub

${\alpha }_{gr}=\arcsin (n\sin (\omega -\arcsin \frac{1}{n})).$

Jeżeli dany pryzmat ma być użyty jako równoramienny pryzmat odbiciowy, w którym światło pada prostopadle na podstawę, by zaszło w nim całkowite wewnętrzne odbicie, to kąt przy podstawie tego pryzmatu musi spełniać warunek:

$\sin \omega >\frac{1}{n}.$

Zobacz też

• rozszczepienie światła
• siatka dyfrakcyjna
• tęcza
• urządzenie optyczne
• węgielnica pryzmatyczna