Półokrąg

Rys. 1. Punkt B poruszający się po półokręgu (łuku ABC) będącym częścią okręgu o środku O. Końce tego półokręgu leżą na odcinku AC. Odcinek AB to promień wodzący punktu B względem punktu A. Odcinek CB to promień wodzący punktu B względem punktu C. Kąt ABC oparty na średnicy AC jest prosty (zob. twierdzenie Talesa).

Rys. 2

Półokrąg – łuk okręgu wyznaczony przez kąt środkowy o mierze 180°. Końce półokręgu leżą więc na jednej średnicy. Promieniem półokręgu jest promień okręgu, którego częścią jest półokrąg.

Twierdzenie o kącie wpisanym w półokrąg

Szablon:Osobny artykuł Twierdzenie to, przypisywane Talesowi, mówi że każdy kąt wpisany w półokrąg oparty na jego podstawie jest kątem prostym.

Wyznaczanie średnich

Wykorzystując właściwości półokręgu, można konstrukcyjnie wyznaczyć średnie z dwóch liczb $a$ i $b.$

Średnia arytmetyczna

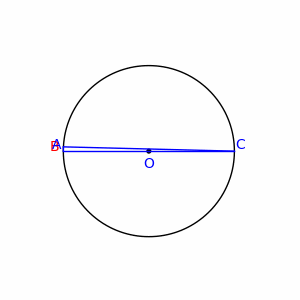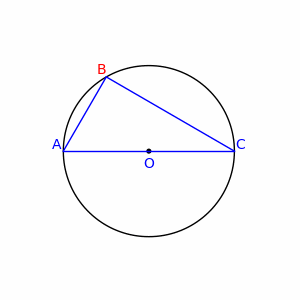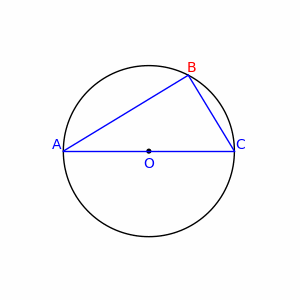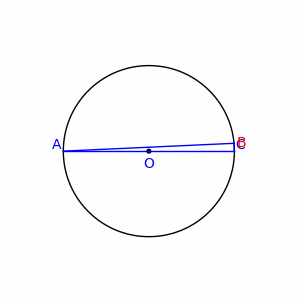
Należy skonstruować półokrąg o podstawie równej $a+b.$ Promień tego półokręgu jest średnią arytmetyczną z obu liczb (rys. 2 – czerwona linia)

$c=\frac{a+b}{2}.$

Średnia geometryczna

Konstruując półokrąg taki sam jak w poprzednim przykładzie, należy narysować odcinek o początku w miejscu zetknięcia się odcinków o długościach $a$ i $b,$ prostopadły do podstawy, o końcu leżącym na łuku półokręgu. Długość tego odcinka jest równa średniej geometrycznej liczb $a$ i $b$ (rys. 2 – brązowa linia)

$d=\sqrt{ab}.$

Można to wykazać, wykorzystując twierdzenie Pitagorasa oraz fakt, że kąt oparty na odcinku o długości $a+b$ jest kątem prostym.

Zobacz też

• konstrukcje geometryczne

Bibliografia

• Szablon:Cytuj książkę
• Szablon:Cytuj książkę

Linki zewnętrzne

• Szablon:Cytuj stronę
• Szablon:Cytuj stronę