Domki i studnie

Domki i studnieSzablon:Odn – zagadka matematyczna, której współczesna wersja może mieć następujące brzmienie: Szablon:Cytat
Formalnie łamigłówka odpowiada na pytanie czy pełny graf dwudzielny jest płaskiSzablon:Odn.
Historia
Przegląd historii zagadki podał David E. Kullman w 1979 stwierdzając, że większość publikacji na temat tego problemu określa go jako „starożytny”Szablon:Odn. Najwcześniejszą wersję, którą odnalazł Kullman, opublikował Henry Ernest Dudeney w 1917Szablon:Odn. Tę samą zagadkę Dudeney opublikował wcześniej w 1913 w The Strand Magazine podkreślając, że jest ona bardzo stara, lecz ją uwspółcześnił dzięki zastosowaniu „wody, gazu i elektryczności”Szablon:Odn.
W innych starych wersjach zagadki należało wytyczyć ścieżki od trzech domów do trzech studni[1], kościoła, knajpy i studni[2] lub gołębnika, studni i brogu[3].
Zagadka stała się motywacją w teorii grafów nad wprowadzeniem pojęcia grafu planarnego[4].
Rozwiązanie
Nie istnieje rozwiązanie pozwalające na wyznaczenie dziewięciu połączeń, w którym linie by się nie przecinałySzablon:Odn. Treść zagadki sprowadza się do utworzenia pełnego dwudzielnego grafu Szablon:Odn. Dowód nierozwiązywalności zagadki sprowadza się do wykazania, że nie jest planarnySzablon:Odn. Ów graf wraz z są elementarnymi grafami nieplanarnymiSzablon:Odn. W 1930 Kazimierz Kuratowski opublikował twierdzenie, w którym stwierdził, że graf jest planarny jeśli nie zawiera w sobie lub Szablon:Odn.
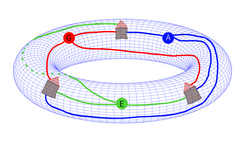
Inne powierzchnie
Możliwość rozrysowania grafu bez przecięć zależy od rozmaitości topologicznej, na której jest on umieszczanySzablon:Odn. Takim przykładem jest torus, na którym graf można narysować bez przecinających się liniiSzablon:Odn.