Całkowanie numeryczne

Całkowanie numeryczne – metoda numerycznaSzablon:R polegająca na przybliżonym obliczaniu całek oznaczonych. Termin kwadratura numeryczna, często po prostu kwadratura, jest synonimem całkowania numerycznego, w szczególności w odniesieniu do całek jednowymiarowych. Dwu- i wielowymiarowe całkowania nazywane są czasami kubaturami, choć nazwa kwadratura odnosi się również do całkowania w wyższych wymiarach.

Proste metody całkowania numerycznego polegają na przybliżeniu całki za pomocą odpowiedniej sumy ważonej wartości całkowanej funkcji w kilku punktach. Aby uzyskać dokładniejsze przybliżenie dzieli się przedział całkowania na niewielkie fragmenty. Ostateczny wynik jest sumą oszacowań całek w poszczególnych podprzedziałach. Najczęściej przedział dzieli się na równe podprzedziały, ale bardziej wyszukane algorytmy potrafią dostosowywać krok do szybkości zmienności funkcji.

Metoda prostokątów

Najprostsza z metod kwadraturowych polega na zastosowaniu wzoru

$\underset{x_0}{\overset{x_n}{\int }}f(x)\approx h\sum _{i=0}^{n-1}f(x_i+\alpha h),h=\frac{x_n-x_0}{n},$

w którym $n$ jest liczbą podprzedziałow o długości $h.$

Metoda ta ma trzy warianty:

• lewych prostokątów, gdy $\alpha =0,$
• średnich prostokątów, gdy $\alpha =\frac{1}{2}$   – ten wariant daje najlepsze przybliżenie,
• prawych prostokątów, gdy $\alpha =1.$

Istnieje oczywiście wariant ogólny, gdy $\alpha \in [0,1].$

Metoda trapezów

Metoda trapezów polega na tym, że całkowaną funkcję aproksymujemy liniowo w każdym z podprzedziałów $x_{i+1},x_i,i=0,1,\dots n-1$ o długości $h=\frac{x_n-x_0}{n}.$ Dzięki temu otrzymujemy po wprowadzeniu oznaczenia $f_i\equiv f(x_i)$

$\underset{x_0}{\overset{x_n}{\int }}f(x)dx\approx \sum _{i=0}^{n-1}\frac{h}{2}[f(x_{i+1})+f(x_i))]=h(\frac{1}{2}{f}_0+f_1+f_2+\dots +f_{n-1}+\frac{1}{2}{f}_n).$

Oszacowanie błędu tej metody wynosi

$R_n=|\underset{a}{\overset{b}{\int }}f(x)dx-S_n|⩽\frac{(b-a{)}^3{M}^{\prime }\text{'}}{12n^2},$

gdzie:

$M^{\prime }\text{'}=\underset{⟨a,b⟩}{\max }|f^{\prime }\text{'}|.$

Metoda parabol (Simpsona)

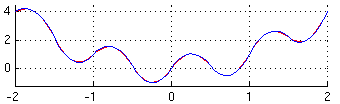
Ta metoda wymaga podzielenia przedziału całkowania na parzystą liczbę $2n$ podprzedziałów, tzn.

$h=\frac{x_{2n}-x_0}{2n},$

$f_i=f(x_i),x_i=x_0+ih,i=0,1,\dots 2n.$

Stosując kwadratową interpolację Lagrange’a na dwu sąsiadujących podprzedziałach, otrzymujemy

$\underset{x_i}{\overset{x_{i+2}}{\int }}f(x)dx\approx \frac{h}{3}[f_i+4f_{i+1}+f_{i+2}],$

$\underset{x_0}{\overset{x_{2n}}{\int }}f(x)dx\approx \frac{h}{3}[f_0+f_{2n}+4(f_1+f_3+\dots +f_{2n-1})+2(f_2+f_4+\dots f_{2n-2})].$

Przy całkowaniu funkcji $f(x)\in C^{(4)}$ na przedziale $[a,b]$ błąd metody wynosi

$R=-\frac{(b-a)h^4}{180}{f}^{IV}(x),x\in [a,b].$

Metoda Gaussa

Szablon:Osobny artykuł Istotne podwyższenie dokładności wzorów kwadraturowych można uzyskać, stosując metodę GaussaSzablon:R. Jej istota polega na minimalizacji błędu kwadratury przez optymalny wybór położenia węzłów ${\xi }_i$ oraz wartości wag ${\bar{w}}_i$ we wzorze kwadraturowym Szablon:Wzór

w którym $F(\xi )=f(\frac{a+b}{2}+\frac{b-a}{2}\xi ),dx=\frac{b-a}{2}d\xi .$

Dzięki zastosowanemu we wzorze (a) odwzorowaniu $x=\frac{a+b}{2}+\frac{b-a}{2}\xi$ dowolnego przedziału $(a,b)$ na standardowy przedział $(-1,1),$ wzór ten jest uniwersalny ponieważ unikalne wartości ${\bar{w}}_i,{\xi }_i$ można stablicować raz na zawsze.

Obliczenie wartości ${\bar{w}}_i,{\xi }_i,i=1,2,\dots ,n$ można przeprowadzić żądając, aby całkowanie procedurą Gaussa jednomianów $x^k,k=0,1,\dots ,2n-1$ dawało wyniki ścisłe Szablon:Wzór

to znaczy aby było dla $k=0,1,\dots ,2n-1$

${\bar{w}}_1{\xi }_1^k+{\bar{w}}_2{\xi }_2^k+\dots +{\bar{w}}_n{\xi }_n^k=p_k,p_k=\frac{1-(-1{)}^{k+1}}{k+1}.$

Po rozpisaniu otrzymujemy, trudny do rozwiązania, nieliniowy układ $2n$ równań Szablon:Wzór

określający $2n$ wartości ${\bar{w}}_i,{\xi }_i.$

W poniższej tabeli zestawionoSzablon:R obliczone wartości parametrów ${\bar{w}}_i,{\xi }_i$ dla wielomianów stopni $n⩽8.$

$n$	${\xi }_1;{\xi }_n$	${\xi }_2;{\xi }_{n-1}$	${\xi }_3;{\xi }_{n-2}$	${\xi }_4;{\xi }_{n-3}$
1	0
2	$\mp 0,57735027$
3	$\mp 0,77459667$	0
4	$\mp 0,86113631$	$\mp 0,33998104$
5	$\mp 0,90617985$	$\mp 0,53846931$	0
6	$\mp 0,93246951$	$\mp 0,66120939$	$\mp 0,23861919$
7	$\mp 0,94910791$	$\mp 0,74153119$	$\mp 0,40584515$	0
8	$\mp 0,96028986$	$\mp 0,79666648$	$\mp 0,52553242$	$\mp 0,18343464$

$n$	${\bar{w}}_1;{\bar{w}}_n$	${\bar{w}}_2;{\bar{w}}_{n-1}$	${\bar{w}}_3;{\bar{w}}_{n-2}$	${\bar{w}}_4;{\bar{w}}_{n-3}$
1	$2$
2	$1$
3	$0,55555556$	$0,88888889$
4	$0,34785484$	$0,65214516$
5	$0,23692688$	$0,47862868$	$0,56888889$
6	$0,17132450$	$0,36076158$	$0,46791394$
7	$0,12948496$	$0,27970540$	$0,38183006$	$0,41795918$
8	$0,10122854$	$0,22238104$	$0,31370664$	$0,36268378$

Cytowany w literaturzeSzablon:R sposób rozwiązania układu równań (c) polega na spostrzeżeniu, że dla dowolnie przyjętych wartości liczbowych ${\xi }_1<{\xi }_2<\dots <{\xi }_n$ macierz współczynników ${\xi }_i^k,$ pierwszych $n$ równań tego układu, jest macierzą Vandermonde’a. Dzięki temu wiadomo, że istnieje jednoznacznie określone rozwiązanie $w_i,i=1,2,\dots n.$ Kwestią otwartą pozostaje jednak wyznaczenie optymalnych wartości ${\xi }_i.$

W tym celu warunek (b) modyfikuje się do postaci obowiązującej dla wielomianów stopnia $N=n+k,k=0,1,\dots ,n-1.$ Szablon:Wzór

gdzie $P_n(x)$ jest wielomianem stopnia $n.$

Całka we wzorze (d) zeruje się, gdy wielomiany $P_n(x)$ są ortogonalne z jednomianami $x^k$ dla $k<n,$ przy $x\in (-1,1).$ Dokładnie taką własnośćSzablon:R mają wielomiany Legendre’a. Dla nich mamy wtedy zamiast (d) Szablon:Wzór

Ten warunek jest spełniony tożsamościowo dla dowolnych wartości $w_i,$ gdy ${\xi }_i$ są pierwiastkami wielomianu Legendre’a $n$-tego stopnia, wtedy bowiem $P_n({\xi }_i)\equiv 0,i=1,2,\dots n.$

Metody losowe

Do przybliżonego obliczania całki oznaczonej można również wykorzystać metody probabilistyczne. Należy pamiętać jednak, że wynik takiego całkowania jest też zmienną losową.

• Monte Carlo

Idea opiera się na policzeniu pola pod wykresem funkcji dla $f(x)>0$ i odjęciu pola nad wykresem dla $f(x)<0$

• probabilistyczna

$\underset{a}{\overset{b}{\int }}f(x)dx\approx \frac{b-a}{n}\sum _{i=1}^{n}f(x_i),$

$x_i$ jest losowo wybierane z przedziału $<a,b>,$

$n$ określa liczność próbki.

Przykłady

Przykład – metoda prostokątów

Spróbujmy scałkować funkcję $\cos (x)$ na przedziale od 0 do 1. Ponieważ da się ją scałkować analitycznie, znamy dokładny wynik i możemy łatwo obliczać błąd przybliżenia różnych metod całkowania. Z dokładnością do 10 miejsc dziesiętnych prawidłowy wynik wynosi:

$\underset{0}{\overset{1}{\int }}\cos (x)dx=\sin (1)-\sin (0)=0,8414709848.$

Całkowanie numeryczne za pomocą zasady punktu środkowego da nam wynik:

$\underset{0}{\overset{1}{\int }}\cos (x)dx\approx (1-0)\cos \left(\frac{1}{2}\right)=0,8775825619,$

co daje błąd 0,0361115771 (błąd względny 4,3%) – niewielki jak na tak prostą metodę, jednak oczywiście niezadowalający do wielu zastosowań.

Żeby uzyskać lepsze przybliżenia możemy podzielić przedział całkowania:

$\underset{0}{\overset{1}{\int }}\cos (x)dx=\underset{0}{\overset{1/2}{\int }}\cos (x)dx+\underset{1/2}{\overset{1}{\int }}\cos (x)dx\approx$

$\approx (\frac{1}{2}-0)\cos \left(\frac{1}{4}\right)+(1-\frac{1}{2})\cos \left(\frac{3}{4}\right)=0,8503006452$

z błędem bezwzględnym 0,0088296604 lub względnym 1%.

Dzieląc przedział całkowania na więcej fragmentów, możemy uzyskać lepsze przybliżenie:

Liczba części	Wynik	Błąd
		bezwzględny	względny
1	0,8775825619	0,0361115771	4,29%
2	0,8503006452	0,0088296604	1,05%
4	0,8436663168	0,0021953320	0,26%
8	0,8420190672	0,0005480824	0,07%
	0,8414709848	0	0%

Przykład 2

Całkowanie numeryczne przebiegów czasowych. Spróbujmy scałkować spróbkowany przebieg $\sin (t)$ na przedziale od 0 do $4\cdot \pi$ [s]. Oznaczmy częstotliwość próbkowania przebiegu przez $f_p$ [Hz].

Do obliczeń wykorzystamy metodę prostokątów. Średnica podziału $t_p=\frac{1}{f_p}=t_{i+1}-t_i$ wynosi 1. Niech $X_i(t)$ oznacza próbkę po całkowaniu. Każdy wyraz $X_i$ można obliczyć jako sumę częściową:

$X_i=\sum _{n=0}^i{x}_i(t)t_p.$

Zobacz też

• kwadratury Gaussa
• metody Newtona-Cotesa