Algorytm Grahama
Szablon:Algorytm infobox Algorytm Grahama – efektywny algorytm wyszukiwania otoczki wypukłej skończonego zbioru punktów płaszczyzny; nie istnieją warianty dla przestrzeni o wyższych wymiarach. Pomysłodawcą algorytmu jest Ronald Graham[1].
Czasowa złożoność obliczeniowa wynosi
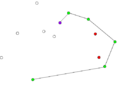
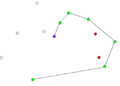
Algorytm przebiega następująco:
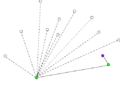
- Wybierz punkt (ozn. O) o najniższej wartości współrzędnej y.
- Przesuń wszystkie punkty tak, by punkt O pokrył się z początkiem układu współrzędnych.
- Posortuj punkty leksykograficznie względem:
- kąta pomiędzy wektorem a dodatnią osią układu współrzędnych,
- odległości punktu od początku układu współrzędnych.
- Wybierz punkt (ozn. S) o najmniejszej współrzędnej y; jeśli kilka punktów ma tę samą współrzędną y, wybierz spośród nich ten o najmniejszej współrzędnej x.
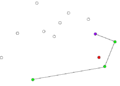
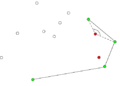
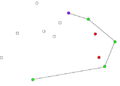
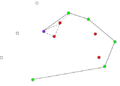
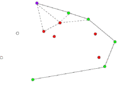
- Przeglądaj listę posortowanych punktów poczynając od punktu S:
- Od bieżącej pozycji weź trzy kolejne punkty (ozn. A, B, C).
- Jeśli punkt B leży na zewnątrz trójkąta AOC, to może należeć do otoczki wypukłej. Przejdź do następnego punktu na liście.
- Jeśli punkt B leży wewnątrz trójkąta AOC, to znaczy, że nie należy do otoczki. Usuń punkt B z listy i cofnij się o jedną pozycję (o ile bieżąca pozycja jest różna od początkowej).
Ze względu na wcześniejsze kroki algorytmu (sortowanie i sposób wybierania analizowanych trójek punktów) dwa z trzech warunków należenia punktu B do trójkąta AOC są spełnione, tj. B leży po „wewnętrznej” względem trójkąta stronie prostych OA i OC. Zatem do stwierdzenia przynależności do trójkąta wystarczy zbadać, po której stronie odcinka AC znajduje się punkt B, w tym celu wykorzystuje się znak iloczynu wektorowego
W praktyce można również utożsamić krok 4. z 1., tzn. przyjąć, że
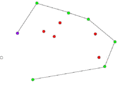
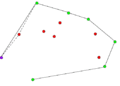
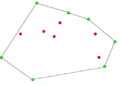
- Przykładowy przebieg algorytmu