Quickhull
Quickhull – algorytm dziel i zwyciężaj z dziedziny geometrii obliczeniowej, który wyznacza otoczkę wypukłą zbioru punktów umieszczonych w przestrzeni o dowolnej liczbie wymiarów (dwa, trzy i więcej). Algorytm jest wzorowany na metodzie sortowania szybkiego (ang. quicksort) i podobnie charakteryzuje go średnia złożoność natomiast pesymistyczna
Algorytm został niezależnie odkryty przez Williama Eddy’ego (1977) i Alexa Bykata (1978) oraz Greena i Silvermana (1979).
Algorytm na płaszczyźnie
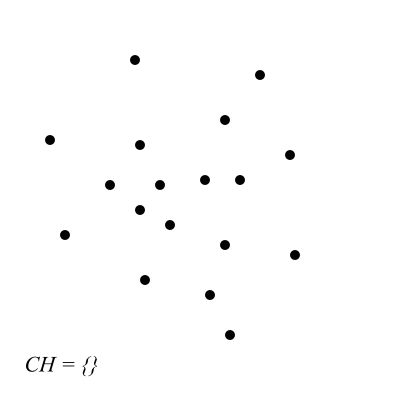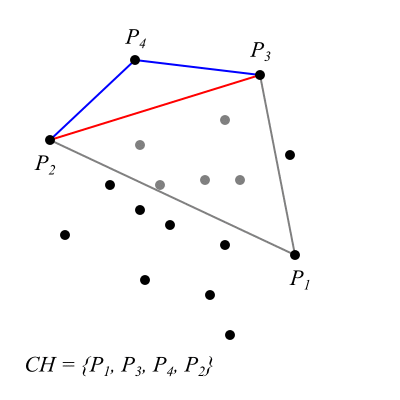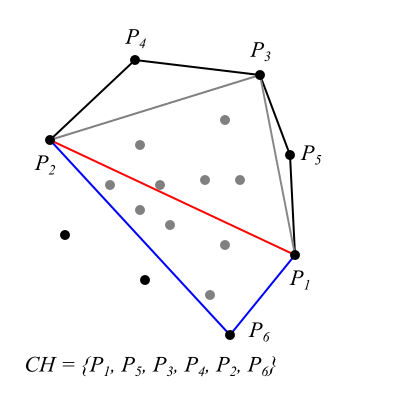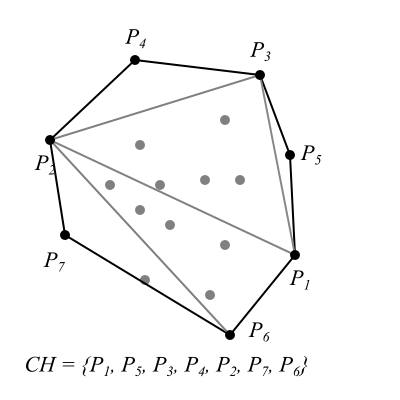
Przygotowanie danych:
- Znajdź w zbiorze punktów dwa skrajne punkty o minimalnej i maksymalnej współrzędnej x ( i ).
- Podziel zbiór punktów na dwa podzbiory S1 i S2 znajdujące się nad i pod prostą
- Wywołaj rekurencyjnie
QuickHull(A, B, S1)iQuickHull(B, A, S2).
Zamiast wyznaczać dwa skrajne punkty, można uwzględnić trzy lub cztery skrajne, otrzymując odpowiednio trójkąt lub czworokąt wypukły i od razu odrzucić wszystkie punkty należące do wnętrza figur. Wówczas procedurę QuickHull należy wywołać dla każdego boku figury, uprzednio dzieląc odpowiednio zbiór punktów.
Procedura QuickHull jako argumenty przyjmuje dwa punkty i wyznaczające prostą oraz zbiór rozpatrywanych punktów:
- Jeśli jest pusty – koniec.
- Jeśli ma jeden element, ten punkt należy do otoczki – koniec.
- W przeciwnym razie:
- Znajdź w punkt najbardziej oddalony od prostej Ten punkt należy do otoczki wypukłej.
- Odrzuć wszystkie punkty z wnętrza trójkąta nie mogą należeć do otoczki.
- Znajdź zbiór S1 punktów znajdujących się po prawej stronie prostej oraz analogiczny zbiór S2 dla prostej (Stronę określa znak równania ogólnego prostej).
- Wywołaj rekurencyjnie
QuickHull(A, C, S1)orazQuickHull(B, C, S2).
Pseudokod
procedure otoczka(punkty)
begin
A := skrajny lewy punkt
B := skrajny prawy punkt
s1 := zbiór punktów po prawej stronie AB
s2 := zbiór punktów po lewej stronie AB
return [A] + QuickHull(A, B, s1) + [B] + QuickHull(B, A, s2);
end;
procedure QuickHull(A, B, punkty)
begin
C := najbardziej odległy punkt od prostej AB
s1 := zbiór punktów znajdujących się na prawo od prostej AC
s2 := zbiór punktów znajdujących się na prawo od prostej CB
return QuickHull(A, C, s1) + [C] + QuickHull(C, B, s2);
end;