Metoda strzałów

Metoda strzałów – metoda rozwiązywania zagadnienia brzegowego przez zastąpienie go zagadnieniem początkowym.

Zagadnienia brzegowego równania różniczkowego drugiego rzędu metoda przedstawia się następująco

$y^{″}(t)=f(t,y(t),y^{\prime }(t)),y(t_0)=y_0,y(t_1)=y_1.$

Niech $y_a(t)$ oznacza rozwiązanie problemu początkowego

$y^{″}(t)=f(t,y(t),y^{\prime }(t)),y(t_0)=y_0,y^{\prime }(t_0)=a.$

Zdefiniujmy funkcje $F(a)$ jako różnicę między $y_a(t)$ a ustaloną wartością brzegową $y_1$

$F(a)=y_a(t_1)-y_1.$

Jeśli problem brzegowy ma rozwiązanie wtedy $F$ ma pierwiastek, i pierwiastek ten jest wartością $y^{\prime }(t_0),$ która daje rozwiązanie $y(t)$ problemu brzegowego.

Zwykłe metody znajdowania pierwiastków, takie jak metoda bisekcji, metoda Newtona mogą zostać użyte do znalezienia $a.$

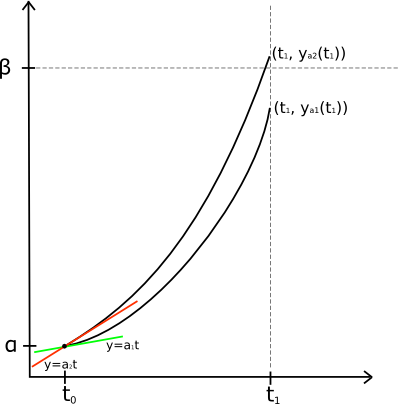
Ilustracja graficzna

Na poniższym rysunku widać, że rozwiązanie problemu początkowego dla dobrze dobranego parametru $a$ jest w przybliżeniu równe rozwiązaniu problemu brzegowego.

Kolorowe linie to styczne funkcji $y_a(t)$ w punkcie $(t_0,y_0)$ dla różnych $a.$