Indeks geometryczny

W chemii koordynacyjnej, strukturalnej oraz krystalografii indeks geometryczny lub parametr strukturalny $(\tau )$ jest liczbą w zakresie 0-1, która informuje o geometrii wokół atomu centralnego cząsteczki (zwykle centrum koordynacji). Pierwszy taki parametr dla związków 5-koordynacyjnych został zaproponowany w 1984 roku. Później opracowano również parametry dla związków 4-koordynacyjnych. Opracowana została również aplikacja on-line do wyznaczania indeksów geometrycznych na podstawie strukturalnych plików 3D.

Związki 5-koordynacyjne

By ocenić, czy geometria centrum koordynacji o LK = 5 zbliżona jest bardziej do bipiramidy trygonalnej, czy piramidy kwadratowej Addison et al. zaproponowali w 1984 roku parametr ${\tau }_5$ (w oryginalnej pracy po prostu $\tau$):

${\tau }_5=\frac{\beta -\alpha }{60^{\circ }}\approx -0,01667\alpha +0,01667\beta ,$

gdzie: $\beta >\alpha$ to dwa największe kąty walencyjne centrum koordynacji.

Gdy parametr ${\tau }_5$ jest bliski 0, to geometria zbliżona jest do piramidy kwadratowej, natomiast gdy jest on bliski 1, to geometria zbliża się do bipiramidy trygonalnej:

• 
  Geometria piramidy kwadratowej
  ${\tau }_5=0$
• 
  Geometria bipiramidy trygonalnej
  ${\tau }_5=1$

Związki 4-koordynacyjne

Poprzez analogię, w 2007 roku Yang et al. zaproponowali parametr ${\tau }_4$ dla związków o LK = 4, aby ocenić czy ich geometria jest bardziej zbliżona do płaskiej kwadratowej, czy tetraedrycznej:

${\tau }_4=\frac{360^{\circ }-(\alpha +\beta )}{360^{\circ }-2\theta }\approx -0,00709\alpha -0,00709\beta +2,55,$

gdzie: $\alpha$ i $\beta$ to dwa największe kąty walencyjne centrum koordynacji; $\theta ={\cos }^{-1}(-\frac{1}{3})\approx 109,5^{\circ }$ to kąt tetraedryczny.

Gdy parametr ${\tau }_4$ jest bliski 0, to geometria jest zbliżona do płaskiej kwadratowej, natomiast gdy jest on bliski 1, to geometria zbliża się do tetraedrycznej. Niestety parametr ten (w przeciwieństwie do ${\tau }_5$) nie różnicuje kątów $\alpha$ i $\beta ,$ przez co struktury o znacząco różniących się geometriach mogą mieć identyczną wartość parametru ${\tau }_4.$ By przezwyciężyć tę niedogodność w 2015 roku Okuniewski et al. zaproponowali parametr ${{\tau }_4}^{\prime },$ który przybiera wartości zbliżone do ${\tau }_4,$ jednak lepiej różnicuje rozpatrywane struktury:

${{\tau }_4}^{\prime }=\frac{\beta -\alpha }{360^{\circ }-\theta }+\frac{180^{\circ }-\beta }{180^{\circ }-\theta }\approx -0,00399\alpha -0,01019\beta +2,55$

gdzie: $\beta >\alpha$ to dwa największe kąty walencyjne centrum koordynacji; $\theta ={\cos }^{-1}(-\frac{1}{3})\approx 109,5^{\circ }$ to kąt tetraedryczny.

Wartości graniczne parametrów ${\tau }_4$ i ${{\tau }_4}^{\prime }$ definiują dokładnie te same geometrie skrajne, jednak parametr ${{\tau }_4}^{\prime }$ jest zawsze mniejszy lub równy parametrowi ${\tau }_4,$ przez co nawet niewielkie odchylenia od geometrii tetraedru są bardziej zauważalne. Jeżeli dla kompleksu tetraedrycznego wartość parametru ${{\tau }_4}^{\prime }$ jest mała, to należy sprawdzić, czy w obrębie centrum koordynacji nie występują dodatkowe oddziaływania. Przykładowo dla kompleksów rtęci(II) udało się w ten sposób odnaleźć oddziaływania Hg···π.

• 
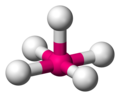
  Geometria płaska kwadratowa
  ${\tau }_4={{\tau }_4}^{\prime }=0$
• 
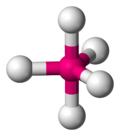
  Geometria huśtawki
  ${\tau }_4\approx 0,43,$ ${{\tau }_4}^{\prime }\approx 0,24$
• 
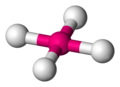
  Geometria tetraedryczna
  ${\tau }_4={{\tau }_4}^{\prime }=1$