Budowa gwiazdy

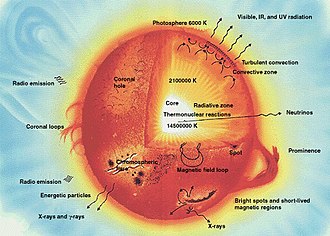
Budowa gwiazdy wielkości Słońca

Budowa gwiazdy – gwiazdy o różnej masie i wieku mają różne struktury wewnętrzne. Modele gwiezdnej struktury opisują szczegółową strukturę wewnętrzną gwiazdy i zawierają szczegółowe prognozy dotyczące jasności, koloru i przyszłej ewolucji gwiazdy. Przez większość czasu gwiazda pozostaje w stanie równowagi między zapadaniem grawitacyjnym a ciśnieniem gazu starającym się przeciwdziałać kolapsowi.

Jednym z modeli gwiazdy w równowadze hydrodynamicznej jest model Newtona gwiazdy. W modelu tym dla kuli gazu o promieniu r źródłem grawitacji jest masa w niej zawarta

$m(r)=4\pi \underset{0}{\overset{r}{\int }}{r^{\prime }}^{2}d{r}^{\prime }\rho (r^{\prime }).$

Masa ta na powierzchni jest źródłem przyśpieszenia grawitacyjnego

$g(r)=G_N\frac{m(r)}{r^2}.$

Przyjmując sferyczną symetrię gwiazdy, jej element można przedstawić jako wycinek sfery o powierzchni S i grubości dr:

$dV=Sdr.$

Na mały element masy:

$dm=\rho (r)dV=\rho (r)Sdr$

działa siła grawitacji oraz równoważąca ją siła wynikająca z różnicy ciśnień:

$\delta F=g(r)dm=g(r)\rho (r)Sdr,$

$\delta F=F(r+dr)-F(r)=SdP.$

Daje to równania

$\frac{dP}{dr}=-G_N\frac{m(r)\rho (r)}{r^2},$

$\frac{dm}{dr}=4\pi \rho (r)r^2.$

Równania te należy uzupełnić równaniem stanu opisującym zależność ciśnienia od odległości od środka gwiazdy. Ciśnienie panujące w gazie/plazmie określane jest głównie przez temperaturę i gęstość:

$P=P(\rho ,T).$

Przy zadanych warunkach początkowych (np. gęstość ρ_c w centrum gwiazdy) jest to układ równań różniczkowych, którego rozwiązanie da rozkład masy w gwieździe m(r), gęstości ρ(r) czy ciśnienia P(r). Znikanie ciśnienia P(R)=0 dla r=R wyznacza promień gwiazdy R a M=m(R) masę gwiazdy.

Równania te należy uzupełnić równaniami opisującymi wytwarzanie i transport energii w gwieździe. W wyniku reakcji syntezy termojądrowej w warstwie odległej o r od centrum gwiazdy produkowana jest gęstość energii ε(r)=ρ(r) p_m w jednostce czasu (gęstość mocy promieniowania). p_m jest mocą promieniowaną przez jednostkową masę. Na powierzchni sfery 4πr² wysyłane jest promieniowanie jasność, którego jest równa L(r). Moc promieniowania produkowanego przez warstwę między promieniem r i r+dr jest równe 4πr²ε(r). Promieniowanie to daje jasność dL. Bilans energetyczny daje więc równanie:

$\frac{dL}{dr}=4\pi r^2ϵ(r)=4\pi r^2\rho (r)p_m.$

Płynący z wnętrza strumień energii jest konsekwencją różnicy temperatur

$j(r)=-K\frac{dT}{dr},$

gdzie K jest przewodnictwem cieplnym ośrodka (plazmy). Wysyłane promieniowanie przez sferę o promieniu r wywołane jest przez strumień energii

$L(r)=4\pi r^{2}j(r).$

Rozkład temperatury T(r) i promieniowania gwiazdy L(r) opisany jest więc dodatkowymi równaniami różniczkowymi:

$K\frac{\text{d}T}{\text{d}r}=-\frac{L}{4\pi r^2},$

$\frac{\text{d}L}{\text{d}r}=4\pi r^2ϵ(r)=4\pi r^2\rho (r)p_m.$

Przewodnictwo cieplne w gwieździe nie jest stałe. Zależy ono silnie od mechanizmu transportu energii, od temperatury i gęstości wewnątrz gwiazdy.

Równania gwiazdy należy więc uzupełnić równaniem na przewodnictwo cieplne ośrodka

$K=K(\rho ,T).$

Jeżeli przewodnictwo cieplne zdominowane jest przez promieniowanie (gaz fotonowy) to:

$K=\frac{4}{3}c\lambda a{T}^3,$

gdzie σ=a c/4 jest współczynnikiem występującym w prawie Stefana-Boltzmanna (promieniowanie ciała doskonale czarnego), a

$\lambda =\frac{1}{\rho \kappa }$

jest średnią drogą swobodną fotonu w plazmie, κ jest współczynnikiem nieprzeźroczystości ośrodka.

W plazmie gwiazdy gdzie dominuje gaz elektronowy droga swobodna fotonu zależy od gęstości elektronów n_e i przekroju czynnego σ_e na rozpraszanie fotonów na elektronach (rozpraszanie Thomsona)

$\lambda =\frac{1}{\rho \kappa }=\frac{1}{n_e{\sigma }_e}.$

Dla przykładu, we wnętrzu Słońca dla gęstości 10⁴ kg m⁻³ średnia droga fotonu wynosi około 10⁻⁵ m. Wnętrze gwiazdy nie jest przezroczyste dla fotonów, staje się przezroczyste dopiero w warstwie między R_γ=R-λ(R_γ) a promieniem gwiazdy R gdzie droga swobodna fotonów jest większa od rozpraszającej warstwy plazmy. Promień R_γ nazywamy promienień fotosfery (fotosfera). Jest to widoczny promień np. Słońca. Droga swobodna neutrin w większości gwiazd jest większa niż promień gwiazdy (wyjątkiem jest młoda gwiazda neutronowa). Neutrina niosą więc informację z samego centrum gwiazdy gdzie zachodzą reakcje syntezy jądrowej.

Linki zewnętrzne

• Variational Principles for Stellar Structure, Dallas C. Kennedy, Sidney A. Bludman, 1996