Rzut ukośny (fizyka)

Ilustracja trajektorii rzutu ukośnego

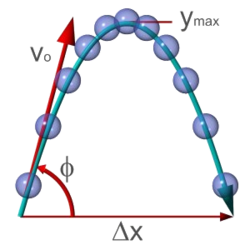
Rzut ukośny – ruch w jednorodnym polu grawitacyjnym z prędkością początkową o kierunku ukośnym do kierunku pola. Ruch ten odpowiada ruchowi ciała rzuconego pod kątem do poziomu. Za rzut ukośny uznaje się też ruch ciała w kierunku ukośnym do jednorodnego pola elektrycznego.

Rzut ukośny w przypadku braku oporów ośrodka można rozważać jako ruch składający się z rzutu pionowego w górę oraz ruchu jednostajnego prostoliniowego.

Pole grawitacyjne

Działanie rzutu ukośnego na strumieniu wody

W artykule przyjęto kartezjański układ współrzędnych (x, y) z osią y równoległą do kierunku linii sił pola o zwrocie przeciwnym do pola, czyli ku górze, oraz osią x, równoległą do składowej poziomej ruchu i tym samym prostopadłą do kierunku linii pola.

Poniższe wzory są prawdziwe dla obszarów ruchu znacznie mniejszych od rozmiarów Ziemi bądź innego ciała niebieskiego, na którym ruch się odbywa, oraz przy zaniedbaniu oporu i wyporu atmosfery.

Warunki początkowe

Prędkość początkową można określić podając jej wartość $v_0$ oraz kąt $\alpha ,$ pod jakim zostało rzucone ciało. Równoważnym sposobem jest podanie prędkości składowych: poziomej $v_{0x}$ i pionowej $v_{0y}.$ Między wielkościami w obu sposobach zachodzą związki:

$v_{0y}=v_0\cdot \sin \alpha ,$

$v_{0x}=v_0\cdot \cos \alpha .$

Dynamika ruchu

Przyjmuje się, że na ciało działa wyłącznie siła grawitacji, skierowana pionowo w dół, co wyrażają wzory:

$F_y=-mg,$

$F_x=0.$

Składowe przyspieszenia są równe:

$a_y=\frac{F_y}{m}=-g,$

$a_x=\frac{F_x}{m}=0.$

Prędkości

Prędkość chwilową w kierunku pionowym po czasie $t$ określa wzór:

$v_y=v_{0y}-g\cdot t=v_0\cdot \sin \alpha -g\cdot t.$

Prędkość chwilowa w kierunku poziomym jest równa prędkości początkowej w tymże kierunku, a więc jest stała podczas całego ruchu:

$v_x=v_0\cdot \cos \alpha =const.$

Czas wznoszenia oraz lotu

Prędkość chwilowa w kierunku pionowym w momencie osiągnięcia przez ciało maksymalnej wysokości jest równa zeru, dlatego czas wznoszenia $t_w$ wynosi:

$t_w=\frac{v_{0y}}{g}=\frac{v_0\cdot \sin \alpha }{g}.$

Czas lotu ciała $t_c,$ przy założeniu, że upadnie ono na tej samej wysokości, co rozpoczęło ruch, jest podwojonym czasem wznoszenia:

$t_c=2\cdot t_w=\frac{2\cdot v_0\cdot \sin \alpha }{g}.$

Maksymalna wysokość oraz zasięg

Maksymalna wysokość na jaką wzniesie się ciało:

$h_{max}=v_{0y}\cdot t_w-\frac{g\cdot t_w^2}{2}=\frac{g\cdot t_w^2}{2}=\frac{(v_0\cdot \sin \alpha {)}^2}{2\cdot g}.$

Zasięg rzutu:

$z=v_x\cdot t_c=\frac{2\cdot v_0^2\cdot \sin \alpha \cdot \cos \alpha }{g}=\frac{v_0^2\cdot \sin 2\alpha }{g}.$

Łatwo zauważyć, że dla określonej prędkości początkowej zasięg będzie najdalszy, jeśli $\alpha =45^{\circ }$

Położenie

Przyjmując za początek ruchu początek kartezjańskiego układu współrzędnych, położenie ciała po czasie $t$ określają równania:

$\{\begin{array}{c}x(t)=v_{0}t\cos \alpha \\ y(t)=v_{0}t\sin \alpha -\frac{g{t}^2}{2}\end{array}.$

Równanie toru rzutu ukośnego w układzie (X,Y):

$y=x\mathrm{tg}\alpha -\frac{g}{2v_0^2{\cos }^2\alpha }{x}^2.$

Równanie to jest równaniem paraboli o ramionach zwróconych w dół, tj. posiadającej maksimum globalne.

Dodatkowe informacje

Mówiąc o rzucie ukośnym bez podania warunków, przyjmuje się zwykle ruch w ziemskim polu grawitacyjnym na średniej szerokości geograficznej i na poziomie morza; pole grawitacyjne ma wówczas przyspieszenie g = 9,81 m/s². Pomija się przy tym opór i wypór powietrza oraz niejednorodność pola grawitacyjnego.

Pole elektryczne

Powyższe wzory można zastosować do jednorodnego pola elektrycznego zastępując przyspieszenie ziemskie przyspieszeniem ciała w polu elektrycznym:

$a=\frac{qE}{m},$

gdzie:

$q$ – ładunek elektryczny ciała,

$E$ – natężenie pola elektrycznego,

$m$ – masa ciała.

Szczególne przypadki

Gdy ciało rzucone jest poziomo, rzut ukośny staje się rzutem poziomym. Dla tego przypadku $v_{0y}=v_0\sin \alpha =0$ oraz $v_0\ne 0,$ $h_{max}>0,$ skąd wynika $\sin \alpha =0,$ czyli $\alpha =0^{\circ }.$

Gdy ciało rzucone jest pionowo, rzut ukośny staje się rzutem pionowym. Dla tego przypadku $v_{0x}=v_0\cos \alpha =0$ oraz $v_0\ne 0,$ skąd wynika $\cos \alpha =0,$ czyli $\alpha =90^{\circ }.$

Gdy prędkość początkowa jest równa zeru, to rzut jest spadkiem swobodnym. Dla tego przypadku $v_{0x}=0,$ $v_{0y}=0$ oraz $h_{max}>0.$

Linki zewnętrzne

• Szablon:Otwarty dostęp Jakub Pokrywka, Rzut ukośny, Poznański Portal Matematyczny, matematyka.poznan.pl, 5 czerwca 2016 [dostęp 2024-10-05].