Plik:Riemann sphere1.jpg

Z testwiki
Przejdź do nawigacji Przejdź do wyszukiwania
Rozmiar pierwotny (1280 × 1024 pikseli, rozmiar pliku: 215 KB, typ MIME: image/jpeg)

Ten plik znajduje się w Wikimedia Commons i może być używany w innych projektach. Poniżej znajdują się informacje ze strony opisu tego pliku.

Ta ilustracja ma także wersję wektorową („SVG”).
Zaleca się wykorzystywanie w galeriach dostępnej wersji wektorowej zamiast obecnej.
File:Riemann sphere1.jpg → File:Riemann sphere1.svg
Więcej o grafice wektorowej przeczytasz w artykule Przenoszenie grafik Commons do formatu SVG.
Dostępna jest także informacja o obsłudze grafik SVG przez MediaWiki.
W innych językach
Alemannisch ∙ العربية ∙ беларуская (тарашкевіца) ∙ български ∙ বাংলা ∙ català ∙ нохчийн ∙ čeština ∙ dansk ∙ Deutsch ∙ Ελληνικά ∙ English ∙ British English ∙ Esperanto ∙ español ∙ eesti ∙ euskara ∙ فارسی ∙ suomi ∙ français ∙ Frysk ∙ galego ∙ Alemannisch ∙ עברית ∙ हिन्दी ∙ hrvatski ∙ magyar ∙ հայերեն ∙ Bahasa Indonesia ∙ Ido ∙ italiano ∙ 日本語 ∙ ქართული ∙ 한국어 ∙ lietuvių ∙ македонски ∙ മലയാളം ∙ Bahasa Melayu ∙ မြန်မာဘာသာ ∙ norsk bokmål ∙ Plattdüütsch ∙ Nederlands ∙ norsk nynorsk ∙ norsk ∙ occitan ∙ polski ∙ prūsiskan ∙ português ∙ português do Brasil ∙ română ∙ русский ∙ sicilianu ∙ Scots ∙ slovenčina ∙ slovenščina ∙ српски / srpski ∙ svenska ∙ தமிழ் ∙ ไทย ∙ Türkçe ∙ татарча / tatarça ∙ українська ∙ vèneto ∙ Tiếng Việt ∙ 中文 ∙ 中文（中国大陆） ∙ 中文（简体） ∙ 中文（繁體） ∙ 中文（马来西亚） ∙ 中文（新加坡） ∙ 中文（臺灣） ∙ +/−
Nowa grafika

Opis

Opis

Sphère de Riemann, démonstration de la projection

English: rendering of the graph of the Sphere of Rieman
Źródło Praca własna. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV.
Autor Jean-Christophe BENOIST 


//------------------------------------------------------------------------
#version 3.6;
global_settings {  assumed_gamma 1 }
//------------------------------------------------------------------------
#include "colors.inc"
#include "textures.inc"
#include "glass.inc"
#include "metals.inc"
#include "golds.inc"
#include "stones.inc"
#include "woods.inc"
#include "shapes.inc"
#include "shapes2.inc"
#include "functions.inc"
#include "math.inc"          
#include "transforms.inc"
//------------------------------------------------------------------------
#declare Camera_0 = camera {                                 // xy-view
                             angle 20
                             location  <8.0 , 8.0 ,-24.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }

#declare Camera_1 = camera {                                // diagonal view
                             angle 9
                             location  <15.0 ,15 ,-60.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }
#declare Camera_2 = camera {                               // yz-view
                             angle 20          
                             location  <31.0 , 7.0 ,1.0>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }
#declare Camera_3 = camera { 
                             angle 20
                             location  < 0.0 , 37.5 ,-0.0001>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }

camera{Camera_0}

//------------------------------------------------------------------------
// sun -------------------------------------------------------------------
light_source{<3000,5500,-1000> color White }
// sky -------------------------------------------------------------------
sky_sphere{ pigment{ gradient <0,1,0>
                     color_map{ [0   color rgb<1,1,1>         ]//White
                                [0.4 color rgb<1,1,1>]  //~Navy
                                [0.6 color rgb<1,1,1>]  //<0.14,0.14,0.56>]//~Navy
                                [1.0 color rgb<1,1,1>         ]//White
                              }
                     scale 2 }
           } // end of sky_sphere 
//------------------------------------------------------------------------
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
//------------------------------ the Axes --------------------------------
//------------------------------------------------------------------------
#macro Axis_( AxisLen, Dark_Texture,Light_Texture) 
 union{
    cylinder { <0,-AxisLen-3,0>,<0,AxisLen,0>,0.017
               texture{checker texture{Dark_Texture } 
                               texture{Light_Texture}
                       translate<0.1,0,0.1>}
             }
    cone{<0,AxisLen,0>,0.1,<0,AxisLen+0.3,0>,0
          texture{Dark_Texture}
         }
     } // end of union                   
#end // of macro "Axis()"
//------------------------------------------------------------------------
#macro AxisXYZ( AxisLenX, AxisLenY, AxisLenZ, Tex_Dark, Tex_Light)
//--------------------- drawing of 3 Axes --------------------------------
union{
#if (AxisLenX != 0)
 object { Axis_(AxisLenX, Tex_Dark, Tex_Light)   rotate< 0,0,-90>}// x-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark} 
          scale 0.5 translate <AxisLenX+0.05,0.4,-0.10>}
#end // of #if 
#if (AxisLenY != 0)
 object { Axis_(AxisLenY, Tex_Dark, Tex_Light)   rotate< 0,0,  0>}// y-Axis
 text   { ttf "arial.ttf",  "z",  0.15,  0  texture{Tex_Dark}    
           scale 0.5 translate <-0.55,AxisLenY+0.20,-0.10>}
#end // of #if 
#if (AxisLenZ != 0)
 object { Axis_(AxisLenZ, Tex_Dark, Tex_Light)   rotate<90,0,  0>}// z-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark}
               scale 0.5 translate <-0.55,0.1,AxisLenZ+0.10>}
#end // of #if 
} // end of union
#end// of macro "AxisXYZ( ... )"
//------------------------------------------------------------------------

#declare Texture_A_Dark  = texture {
                               pigment{color rgb<0.5,0.5,0.5>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
#declare Texture_A_Light = texture { 
                               pigment{color rgb<1,1,1>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
                                                                                                              
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                                                              
                                                                                                              
object{ AxisXYZ( 25.0, 0, 25.0, Texture_A_Dark, Texture_A_Dark)} // <<<<<<<<<<<<<<<<< adapt the axes here !!!


#declare        TextScale=0.5;

//-------------------------------------------------- end of coordinate axes


// ground -----------------------------------------------------------------
//---------------------------------<<< settings of squered plane dimensions
#declare RasterScale = 2.0/2;
#declare RasterHalfLine  = 0.03/4;  
#declare RasterHalfLineZ = 0.03/2; 
//-------------------------------------------------------------------------
#macro Raster(RScale, HLine) 
       pigment{ gradient x scale RScale
                color_map{[0.000   color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>*0.2]
                          [1.000   color rgbt<1,1,1,1>*0.2]} }
       finish { ambient 0.15 diffuse 0.85}
 #end// of Raster(RScale, HLine)-macro    
//-------------------------------------------------------------------------
    

plane { <0,1,0>, 0    // plane with layered textures
        texture { pigment{color rgbt<1,1,1,0.7>*1.1}
                  finish {ambient 0.45 diffuse 0.85}}
        texture { Raster(RasterScale,RasterHalfLine ) rotate<0,0,0> }
        texture { Raster(RasterScale,RasterHalfLineZ) rotate<0,90,0>}
        rotate<0,0,0>
        no_shadow
      }
//------------------------------------------------ end of squered plane XZ   



// 
//------------------------------------------------------------------------------------
#include "analytical_g.inc" 





//--------------------------------------------------------------------------
//---------------------------- objects in scene ----------------------------
//--------------------------------------------------------------------------
#default{ finish {ambient 0.15 diffuse 0.85} } // 



//-----------------------------------------------------------------------------------
#declare Rl  = 0.035; // radius of lines  - Radius der Strecken 
#declare Rp  = 0.06; // radius of points - Radius der Punkte 


//------------------------------------------------------------------------------------
// ----------------------------------------------------------------------------------- 

// ----------------------------------------------------------------------------------- 
// ---------------------  Punti e Vettori  - Punkte und Vektoren -  Points and Vectors
//------------------------------------------------------------------------------------

#declare M1 = < 0, 0.0,0.0>;  
#declare R1  = 3;   

#declare M2  = < 0.0,0.0, 0.0>;
#declare Rx  = 3.00;
#declare Ry  = 1.00;
#declare Rz  = 2.00;

#declare P1   = < 3, 0, 0>;
#declare Pi   = < 0, 0, 3>;
#declare PPinf = < 0, 3, 0>;        
#declare PP0   = < 0, -3, 0>;  
#declare P0   = <0,0,0>;

sphere{ P1, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "1",0.1,0 
       scale TextScale rotate<0,0,0> translate P1+<0.2,0.1,-0.2> pigment{ color Red } no_shadow}


sphere{ Pi, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "i",0.1,0 
       scale TextScale rotate<0,0,0> translate Pi+<-0.1,0.1,0.2> pigment{ color Red } no_shadow}
       
       
sphere{ PPinf, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", concat("R(",chr(165),")"),0.1,0 
       scale TextScale rotate<0,0,0> translate PPinf+<-0.1,0.1,0> pigment{ color Red } no_shadow}             
       
       
sphere{ PP0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "R(0)",-0.1,0 
       scale TextScale rotate<0,0,0> translate PP0+<-0.1,0.1,0> pigment{ color Red } no_shadow}         
       
sphere{ P0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "0",-0.1,0 
       scale TextScale rotate<0,0,0> translate P0+<-0.1,0.1,0> pigment{ color Red } no_shadow}           
 
 
//object{ Show_Yxz( M1, Rl/2) pigment{ color Yellow }}
//object{ Show_Yxz( M2, Rl/2) pigment{ color Yellow }}
//------------------------------------------------------------------------------------
// --------------------------------------------------------------- Zeichnen ---------- 
// ---------------------------------------------------------------- Drawing ---------- 

                               
#declare RSphere=
object {
        sphere{ M1, R1                          pigment{ color Yellow transmit 0.6 } finish {phong 0.3}}
}                               
                               
                               
#declare PPlan1 = <4.5,0,0>;     
               
object{ Vector (PPinf, PPlan1, Rl)
         pigment{color Red}}  

sphere{ PPlan1, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan1, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "A",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan1+<0.1,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan1 - PPinf );                      

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "a=R(A)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  
                 






#declare PPlan2 = <-1.5,0,0>;     
               


sphere{ PPlan2, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan2, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "B",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan2+<0.3,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan2 - PPinf );   

object{ Vector (PPinf, Hit_the_Object, Rl)
         pigment{color Red}}                     

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "b=R(B)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  



                 
                 
                 
object {RSphere}

Licencja

Ja, właściciel praw autorskich do tego dzieła, udostępniam je na poniższych licencjach
GNU head Udziela się zgody na kopiowanie, rozpowszechnianie oraz modyfikowanie tego dokumentu zgodnie z warunkami GNU Licencji Wolnej Dokumentacji, w wersji 1.2 lub nowszej opublikowanej przez Free Software Foundation; bez niezmiennych sekcji, bez treści umieszczonych na frontowej lub tylnej stronie okładki. Kopia licencji załączona jest w sekcji zatytułowanej GNU Licencja Wolnej Dokumentacji.
w:pl:Licencje Creative Commons
uznanie autorstwa na tych samych warunkach 		Ten plik udostępniony jest na licencji Creative Commons Uznanie autorstwa – Na tych samych warunkach 3.0.
Wolno:
  • dzielić się – kopiować, rozpowszechniać, odtwarzać i wykonywać utwór
  • modyfikować – tworzyć utwory zależne
Na następujących warunkach:
  • uznanie autorstwa – musisz określić autorstwo utworu, podać link do licencji, a także wskazać czy utwór został zmieniony. Możesz to zrobić w każdy rozsądny sposób, o ile nie będzie to sugerować, że licencjodawca popiera Ciebie lub Twoje użycie utworu.
  • na tych samych warunkach – Jeśli zmienia się lub przekształca niniejszy utwór, lub tworzy inny na jego podstawie, można rozpowszechniać powstały w ten sposób nowy utwór tylko na podstawie tej samej lub podobnej licencji.
Ten szablon został dodany jako element zmiany licencjonowania.
w:pl:Licencje Creative Commons
uznanie autorstwa na tych samych warunkach
Ten plik jest udostępniany na licencji Creative Commons Uznanie autorstwa – na tych samych warunkach 2.5 zlokalizowana, 2.0 zlokalizowana oraz 1.0 zlokalizowana.
Wolno:
  • dzielić się – kopiować, rozpowszechniać, odtwarzać i wykonywać utwór
  • modyfikować – tworzyć utwory zależne
Na następujących warunkach:
  • uznanie autorstwa – musisz określić autorstwo utworu, podać link do licencji, a także wskazać czy utwór został zmieniony. Możesz to zrobić w każdy rozsądny sposób, o ile nie będzie to sugerować, że licencjodawca popiera Ciebie lub Twoje użycie utworu.
  • na tych samych warunkach – Jeśli zmienia się lub przekształca niniejszy utwór, lub tworzy inny na jego podstawie, można rozpowszechniać powstały w ten sposób nowy utwór tylko na podstawie tej samej lub podobnej licencji.
Możesz wybrać, którą licencję chcesz zastosować.

Podpisy

Dodaj jednolinijkowe objaśnienie tego, co ten plik pokazuje

Obiekty przedstawione na tym zdjęciu

przedstawia

Historia pliku

Kliknij na datę/czas, aby zobaczyć, jak plik wyglądał w tym czasie.

Data i czasMiniaturaWymiaryUżytkownikOpis
aktualny17:11, 4 cze 2007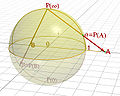Miniatura wersji z 17:11, 4 cze 20071280 × 1024 (215 KB)wikimediacommons>Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO

Poniższa strona korzysta z tego pliku:

Źródło: „https://pl.wiki.beta.math.wmflabs.org/wiki/Plik:Riemann_sphere1.jpg”