Plik:Jordan illustration.png
Z testwiki
Przejdź do nawigacji
Przejdź do wyszukiwania

Rozmiar podglądu – 634 × 599 pikseli. Inne rozdzielczości: 254 × 240 pikseli | 508 × 480 pikseli | 812 × 768 pikseli | 1064 × 1006 pikseli.
Rozmiar pierwotny (1064 × 1006 pikseli, rozmiar pliku: 55 KB, typ MIME: image/png)
Ten plik znajduje się w Wikimedia Commons i może być używany w innych projektach. Poniżej znajdują się informacje ze strony opisu tego pliku.
Opis
| OpisJordan illustration.png |
English: A set (represented in the picture by the region inside the blue curve) is Jordan measurable if and only if it can be well-approximated both from the inside and outside by simple sets (their boundaries are shown in dark green and dark pink respectively). |
| Data | |
| Źródło | Praca własna |
| Autor | Oleg Alexandrov |
| PNG rozwój InfoField |
Licencja
| Public domainPublic domainfalsefalse |
| Ja, właściciel praw autorskich do tej pracy, udostępniam ją jako własność publiczną. Dotyczy to całego świata. W niektórych krajach może nie być to prawnie możliwe, jeśli tak, to: Zapewniam każdemu prawo do użycia tej pracy w dowolnym celu, bez żadnych ograniczeń, chyba że te ograniczenia są wymagane przez prawo. |
Source code (MATLAB)
function main()
% the function whose zero level set and inner and outer approximations will be drawn
f = inline('60-real(z).^2-1.2*imag(z).^2-0.006*(real(z)-6).^4-0.01*(imag(z)-5).^4', 'z');
M=10; i=sqrt(-1); lw=2.5;
figure(1); clf; hold on; axis equal; axis off;
if 1==0
for p=-M:M
for q=-M:M
z=p+i*q;
if f(z)>0
plot(real(z), imag(z), 'r.')
else
plot(real(z), imag(z), 'b.')
end
end
end
end
% draw the zero level set of f
h=0.1;
XX = -M:h:M; YY = -M:h:M;
[X, Y] = meshgrid (XX, YY); Z = f(X+i*Y);
[C, H] = contour(X, Y, Z, [0, 0]);
set(H, 'linewidth', lw, 'EdgeColor', [0;0;156]/256);
% plot the outer polygonal curve
Start=5+6*i; Dir=-i; Sign=-1;
plot_poly (Start, Dir, Sign, f, lw, [139;10;80]/256);
% plot the inner polygonal curve
Sign=1; Start=4+5*i;
plot_poly (Start, Dir, Sign, f, lw, [0;100;0]/256);
% a dummy plot to avoid a matlab bug causing some lines to appear too thin
plot(8.5, 7.5, '*', 'color', 0.99*[1, 1, 1]);
plot(-4.5, -5, '*', 'color', 0.99*[1, 1, 1]);
saveas(gcf, 'jordan_illustration.eps', 'psc2');
function plot_poly (Start, Dir, Sign, f, lw, color)
Current_point = Start;
Current_dir = Dir;
Ball_rad = 0.03;
for k=1:100
Next_dir=-Current_dir;
% from the current point, search to the left, down, and right and see where to go next
for l=1:3
Next_dir = Next_dir*(Sign*i);
if Sign*f(Current_point+Next_dir)>=0 & Sign*f(Current_point+(Sign*i)*Next_dir) < 0
break;
end
end
Next_point = Current_point+Next_dir;
plot([real(Current_point), real(Next_point)], [imag(Current_point), imag(Next_point)], 'linewidth', lw, 'color', color);
round_ball(Current_point, Ball_rad, color'); % just for beauty, to round off some rough corners
Current_dir=Next_dir;
Current_point = Next_point;
end
function round_ball(z, r, color)
x=real(z); y=imag(z);
Theta = 0:0.1:2*pi;
X = r*cos(Theta)+x;
Y = r*sin(Theta)+y;
Handle = fill(X, Y, color);
set(Handle, 'EdgeColor', color);

|
Ta grafika (math) (lub wszystkie grafiki w tym artykule bądź kategorii) powinny zostać przetworzone na grafiki wektorowe jako plik SVG. O zaletach grafik wektorowych można przeczytać na stronie Commons:Media for cleanup. Jeśli wersja SVG tej grafiki jest już dostępna, załaduj ją. Po załadowaniu SVG zamień ten szablon na stronie tej grafiki na szablon {{vector version available|nazwa nowej grafiki.svg}}.
|
Podpisy
Dodaj jednolinijkowe objaśnienie tego, co ten plik pokazuje
A set ( the region inside the blue curve) is Jordan measurable if and only if it can be well-approximated both from the inside and outside by simple sets (their boundaries are shown in dark green and dark pink respectively).
Obiekty przedstawione na tym zdjęciu
przedstawia
Historia pliku
Kliknij na datę/czas, aby zobaczyć, jak plik wyglądał w tym czasie.
| Data i czas | Miniatura | Wymiary | Użytkownik | Opis | |
|---|---|---|---|---|---|
| aktualny | 18:27, 4 lut 2007 | 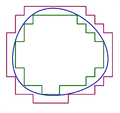 | 1064 × 1006 (55 KB) | wikimediacommons>Oleg Alexandrov | Made by myself with Matlab. {{PD}} |
Lokalne wykorzystanie pliku
Poniższa strona korzysta z tego pliku: