Plik:Conformal mapping from right half plane to unit circle.svg
Z testwiki
Przejdź do nawigacji
Przejdź do wyszukiwania

Wielkość pliku podglądu PNG dla pliku SVG: 800 × 267 pikseli Inne rozdzielczości: 320 × 107 pikseli | 640 × 213 pikseli | 1024 × 341 pikseli | 1280 × 427 pikseli | 2560 × 853 pikseli | 1500 × 500 pikseli.
Rozmiar pierwotny (Plik SVG, nominalnie 1500 × 500 pikseli, rozmiar pliku: 472 KB)
Ten plik znajduje się w Wikimedia Commons i może być używany w innych projektach. Poniżej znajdują się informacje ze strony opisu tego pliku.
Opis
| OpisConformal mapping from right half plane to unit circle.svg |
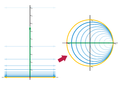
Polski: odwzorowanie równokątne prawej połowy płaszczyzny zespolonej na koło jednostkowe i jego odwrotność |
| Data | |
| Źródło | Praca własna |
| Autor | Adam majewski |
Compare with
-
Conformally map of upper half-plane to unit disk using
-
The point I is variable on [Oy) and (Γ) is a circle going through B and whose center is I. The picture is the inverse of the half-plane y<0 with respect to the circle (Γ)
Licencja
Ja, właściciel praw autorskich do tego dzieła, udostępniam je na poniższej licencji
Ten plik udostępniony jest na licencji Creative Commons Uznanie autorstwa – Na tych samych warunkach 3.0.
- Wolno:
- dzielić się – kopiować, rozpowszechniać, odtwarzać i wykonywać utwór
- modyfikować – tworzyć utwory zależne
- Na następujących warunkach:
- uznanie autorstwa – musisz określić autorstwo utworu, podać link do licencji, a także wskazać czy utwór został zmieniony. Możesz to zrobić w każdy rozsądny sposób, o ile nie będzie to sugerować, że licencjodawca popiera Ciebie lub Twoje użycie utworu.
- na tych samych warunkach – Jeśli zmienia się lub przekształca niniejszy utwór, lub tworzy inny na jego podstawie, można rozpowszechniać powstały w ten sposób nowy utwór tylko na podstawie tej samej lub podobnej licencji.
Long decription
Map from z-plane ( without z=-1 ) to w-plane :

maps right half plane :

to unit disk about the origin :

Maxima CAS src code
/*
b batch file for maxima
There are 2 complex planes :
* w-plane
* z-plane
z is a pont of z-planes
zz is a list of z points
zzz is a list of zz lists
1. draw cufves on z plane
2. draw images of z-curves under h on w plane
3. draw images of w-curves under hi on z plane
http://math.stackexchange.com/questions/114733/mapping-half-plane-to-unit-disk
Adam Majewski
*/
kill(all);
remvalue(all);
/* definitions of functions */
/* map from z to w : w=h(z) */
h(z):=if z=infinity then 1 else (z-1)/(z+1); /* map from z plane to w plane : w = h(z) */
/* inverse of h function maps from w to z : z:hi(w) */
hi(w):= if w=1 then %i*infinity else rectform((1+w)/(1-w));
/* converts complex number into list for draw package */
draw_format(z):= [float(realpart(z)),float(imagpart(z))];
compile(all);
print (" ============== compute =============== ")$
/* curve is a list of points joned by lines */
/* vertical z-lines */
zz : makelist (k*%i/10, k, -200, 200 )$ /* line re(z)=0 */
zz1 : makelist (k*%i/10+1, k, -200, 200 )$ /* line re(z)=1 */
zz2 : makelist (k*%i/10+2, k, -200, 200 )$ /* line re(z)=2 */
/* horizontal z-lines */
zzx : makelist (k/10, k, 0, 400 )$ /* line im(z)=0 */
zzx1 : makelist (%i+k/10, k, 0, 400 )$ /* line im(z)= 1 */
zzx2 : makelist (2*%i+k/10, k, 0, 400 )$ /* line im(z) = 2 */
zzxm1 : makelist (-%i+k/10, k, 0, 400 )$ /* line im(z)=-1 */
zzxm2 : makelist (-2*%i+k/10, k, 0, 400 )$ /* line im(z)=-2 */
/* --------- map from z to w plane using h -------------------------------*/
/* w-curves = images of verticla z-lines */
ww : map(h,zz )$
ww1 : map(h,zz1)$
ww2 : map(h,zz2)$
/* w-curves = images of horizontal z-lines */
wwx:map(h,zzx)$
wwx1:map(h,zzx1)$
wwx2:map(h,zzx2)$
wwxm1:map(h,zzxm1)$
wwxm2:map(h,zzxm2)$
/* map from w to z plane using hi */
zzhi : map(hi,ww)$
zz1hi : map(hi,ww1)$
zz2hi : map(hi,ww2)$
zzxhi : map(hi, wwx)$
zzx1hi : map(hi, wwx1)$
zzx2hi : map(hi, wwx2)$
zzxm1hi : map(hi, wwxm1)$
zzxm2hi : map(hi, wwxm2)$
/* single important points */
z0 : 0; /* origin z=0 */
w0 : h(z0);
z0hi : hi(w0);
zi:infinity; /* point at infinity */
wi:h(zi);
print ("-------------- convert lists of complex points to draw format lists ----------- ")$
zz:map(draw_format,zz)$
ww:map(draw_format,ww)$
zzhi:map(draw_format,zzhi)$
zz1:map(draw_format,zz1)$
ww1:map(draw_format,ww1)$
zz1hi:map(draw_format,zz1hi)$
zz2:map(draw_format,zz2)$
ww2:map(draw_format,ww2)$
zz2hi:map(draw_format,zz2hi)$
/* horizontal z-lines */
zzx : map(draw_format,zzx)$ /* line im(z)=0 */
zzx1 : map(draw_format,zzx1)$ /* line z= 1 */
zzx2 : map(draw_format,zzx2)$ /* line z = 2 */
zzxm1 : map(draw_format,zzxm1)$ /* line z=-1 */
zzxm2 : map(draw_format,zzxm2)$ /* line z=-2 */
zzxhi : map(draw_format,zzxhi)$ /* line im(z)=0 */
zzx1hi : map(draw_format,zzx1hi)$ /* line z= 1 */
zzx2hi : map(draw_format,zzx2hi)$ /* line z = 2 */
zzxm1hi : map(draw_format,zzxm1hi)$ /* line z=-1 */
zzxm2hi : map(draw_format,zzxm2hi)$ /* line z=-2 */
/* images of z-lines */
wwx : map(draw_format,wwx)$ /* image of line im(z)=0 */
wwx1 : map(draw_format,wwx1)$ /* line z= 1 */
wwx2 : map(draw_format,wwx2)$ /* line z = 2 */
wwxm1 : map(draw_format,wwxm1)$ /* line z=-1 */
wwxm2 : map(draw_format,wwxm2)$ /* line z=-2 */
/* points not a list of points */
z0:draw_format(z0);
w0:draw_format(w0);
z0hi:draw_format(z0hi);
/* zi:draw_format(zi); */
wi:draw_format(wi);
print (" ------------------ draw ------------------------------------------------------ ")$
path:"~/maxima/batch/julia/parabolic/z2z/preimages/1/"$ /* pwd */
FileName:"i"$ /* without extension which is the terminal name */
load(draw); /* Mario Rodríguez Riotorto http://www.telefonica.net/web2/biomates/maxima/gpdraw/index.html */
draw(
terminal = 'svg,
file_name = concat(path,FileName),
columns = 3,
dimensions=[1500,500], /* x = y*columns */
gr2d(title = " z plane ",
yrange = [-3,3],
xrange = [-1,5],
points_joined =true,
grid = false,
color = red,
point_size = 0.2,
point_type = filled_circle,
points(zz),
color = blue,
points(zz1),
color = green,
points(zz2),
color = gray,
points(zzx),
points(zzx1),
points(zzx2),
points(zzxm1),
points(zzxm2),
points_joined =false,
color = black,
point_size = 0.8,
key="origin",
points([z0])
),
gr2d(
title = " w plane : w=h(z)= (z-1)/(z+1)",
yrange = [-2.0,2.0],
xrange = [-2.0,2.0],
grid = false,
xaxis = false,
points_joined =true,
color = red,
point_size = 0.2,
point_type = filled_circle,
points(ww),
color = blue,
points(ww1),
color=green,
points(ww2),
color = gray,
points(wwx),
points(wwx1),
points(wwx2),
points(wwxm1),
points(wwxm2),
points_joined =false,
color=black,
point_size = 0.8,
key = "h(origin)",
points([w0]),
color = red,
key="h(infinity)",
points([wi])
),
gr2d(title = " z plane : z=hi(w) = (1+w)/(1-w)",
yrange = [-3,3],
xrange = [-1,5],
grid = false,
xaxis = false,
points_joined =true,
color = red,
point_size = 0.2,
point_type = filled_circle,
points(zzhi),
color = blue,
points(zz1hi),
color = green,
points(zz2hi),
color = gray,
points(zzxhi),
points(zzx1hi),
points(zzx2hi),
points(zzxm1hi),
points(zzxm2hi),
point_size = 0.8,
points_joined =false,
color = black,
key = "hi(h(origin))",
points([z0hi])
)
);
Refeerences
- ↑ Unit disk in wikipedia
- ↑ Mapping half-plane to unit disk?
- ↑ Adam Majewski: fatou-coordinate in maxima-cas
Podpisy
Dodaj jednolinijkowe objaśnienie tego, co ten plik pokazuje
Obiekty przedstawione na tym zdjęciu
przedstawia
Jakaś wartość bez elementu Wikidanych
4 maj 2014
image/svg+xml
6cf65d5aac11eccaff4487314f01fa08e9d225a1
483 418 bajt
500 piksel
1500 piksel
Historia pliku
Kliknij na datę/czas, aby zobaczyć, jak plik wyglądał w tym czasie.
| Data i czas | Miniatura | Wymiary | Użytkownik | Opis | |
|---|---|---|---|---|---|
| aktualny | 16:21, 4 maj 2014 | 1500 × 500 (472 KB) | wikimediacommons>Soul windsurfer | User created page with UploadWizard |
Lokalne wykorzystanie pliku
Poniższa strona korzysta z tego pliku: