Plik:ComponentNewton.jpg

Ten plik znajduje się w Wikimedia Commons i może być używany w innych projektach. Poniżej znajdują się informacje ze strony opisu tego pliku.

|
Ten plik został zastąpiony przez File:Mandelbrot set Component by Newton method.png. Sugerujemy użycie tamtego pliku.
|
|
Opis
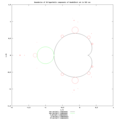
| OpisComponentNewton.jpg |
English: Boundaries of Components of Mandelbrot set by Newton method Polski: Brzeg składowych zbioru Mandelbrot obliczony metodą Newtona |
| Data | |
| Źródło | Own work by uploader ( using Maxima and Gnuplot ) with help of many people ( see references ) |
| Autor | Adam majewski |
Long description
Definition of hyperbolic components ( system of 2 equations)
Boundaries of hyperbolic components for period n of Mandelbrot set are defined by system of equations[1] :

Above system of 2 equations has 3 variables : 
Boundaries are closed curves : cardioids or circles. One can parametrize points of boundaries with angle 
After evaluation of 

Now it can be solved
Solving system of equations
Method of solving system of equation :[2]
- Newton method for solving system of nonlinear equations in more then one variable (Maxima implementation = function mnewton[3] )
- centers of hyperbolic component as an initial approximation
Using Newton method is based on Mark McClure kopia archiwizowana w Wayback Machine's paper "Bifurcation sets and critical curves"[4]
Computing centers of hyperbolic components for given period n:
- compute center for given period n ( Maxima function polyroots[5][6] or allroots [7])
- remove centers for dividers of n. It can be done by dividing polynomials ( Robert Munafo method)[8]
Result of solving
Solving above system gives one point c of each hyperbolic compponent of period n for each angle t ( point w ). Together it gives a list of points
Drawing
Draw a list of points ( on the sceen or to the file using Maxima draw2d function [9])
Set of points looks like curve.
/*
batch file for Maxima
http://maxima.sourceforge.net/
wxMaxima 0.7.6 http://wxmaxima.sourceforge.net
Maxima 5.16.1 http://maxima.sourceforge.net
Using Lisp GNU Common Lisp (GCL) GCL 2.6.8 (aka GCL)
Distributed under the GNU Public License.
based on :
Mark McClure "Bifurcation sets and critical curves" - Mathematica in Education and Research, Volume 11, issue 1 (2006).
*/
start:elapsed_run_time ();
load("mnewton")$
newtonepsilon: 1.e-3;
newtonmaxiter: 100;
load("C:/Program Files/Maxima-5.13.0/share/maxima/5.13.0/share/polyroots/jtroot3.mac")$ /* Raymond Toy http://common-lisp.net/~rtoy/jtroot3.mac */
maperror:false;
fpprec : 16;
/* ---------------- definitions ------------------------------------*/
/* basic funtion */
f(z,c):=z*z+c$
/* */
F(n, z, c) :=
if n=1 then f(z,c)
else f(F(n-1, z, c),c)$
/* */
G(n,z,c):=F(n, z, c)-z$
iMax:100; /* number of points to draw */
dt:1/iMax;
/*
unit circle D={w:abs(w)=1 } where w=l(t)
t is angle in turns ; 1 turn = 360 degree = 2*Pi radians
*/
l(t):=%e^(%i*t*2*%pi);
/* point to point method of drawing */
t:0; /* angle in turns */
/* compute first point of curve, create list and save point to this list */
/* point of unit circle w:l(t); */
w:rectform(ev(l(t), numer)); /* "exponential form prevents allroots from working", code by Robert P. Munafo */
/* period 1 */
p:1;
/* center of component */
ec:G(p,0,c)$
center1:polyroots(ec,c);
nMax1:length(center1);
/* boundary point */
e11:expand(G(p,z,c))$
e12:expand(diff(F(p,z,c),z))$
c1:mnewton([e11, e12-w], [z,c], [center1[1], center1[1]]); /* code by Robert P. Munafo */
nMax1:length(c1);
xx1:makelist (realpart(rhs(c1[1][2])), i, 1, 1);
yy1:makelist (imagpart(rhs(c1[1][2])), i, 1, 1);
/* period 2 */
p:2;
/* center of component */
ec:radcan(G(p,0,c)/G(1,0,c))$ /* code by Robert P. Munafo and all similar beyond */
center2:polyroots(ec,c);
nMax2:length(center2);
/* boundary point */
e21:radcan(G(p,z,c)/G(1,z,c))$
e22:expand(diff(F(p,z,c),z))$
c2:mnewton([e21, e22-w], [z,c], [center2[1], center2[1]]);
xx2:makelist (realpart(rhs(c2[1][2])), i, 1, 1);
yy2:makelist (imagpart(rhs(c2[1][2])), i, 1, 1);
/* period 3 */
p:3;
/* center of component */
ec:radcan(G(p,0,c)/G(1,0,c))$
center3:polyroots(ec,c);
nMax3:length(center3);
/* boundary point */
e31:radcan(G(p,z,c)/G(1,z,c))$
e32:expand(diff(F(p,z,c),z))$
/* */
c3:mnewton([e31, e32-w], [z,c], [center3[1], center3[1]]);
xx3:makelist (realpart(rhs(c3[1][2])), i, 1, 1);
yy3:makelist (imagpart(rhs(c3[1][2])), i, 1, 1);
for n:2 thru nMax3 step 1 do /* all components in 1 list */
block
(
c3:mnewton([e31, e32-w], [z,c], [center3[n], center3[n]]),
xx3:cons(realpart(rhs(c3[1][2])),xx3),
yy3:cons(imagpart(rhs(c3[1][2])),yy3)
);
/* period 4 */
/* center of component */
ec:radcan(G(4,0,c)/G(2,0,c))$
center4:polyroots(ec,c);
nMax4:length(center4);
/* boundary point */
e41:radcan(G(4,z,c)/G(2,z,c))$
e42:expand(diff(F(4,z,c),z))$
c4:mnewton([e41, e42-w], [z,c], [center4[1], center4[1]]);
xx4:makelist (realpart(rhs(c4[1][2])), i, 1, 1);
yy4:makelist (imagpart(rhs(c4[1][2])), i, 1, 1);
for n:2 thru nMax4 step 1 do /* all components in 1 list */
block
(
c4:mnewton([e41, e42-w], [z,c], [center4[n], center4[n]]),
xx4:cons(realpart(rhs(c4[1][2])),xx4),
yy4:cons(imagpart(rhs(c4[1][2])),yy4)
);
/* period 5 */
newtonmaxiter: 200;
/* center of component */
ec:radcan(G(5,0,c)/G(1,0,c))$
center5:polyroots(ec,c);
nMax5:length(center5);
/* boundary point */
e51:radcan(G(5,z,c)/G(1,z,c))$
e52:expand(diff(F(5,z,c),z))$
c5:mnewton([e51, e52-w], [z,c], [center5[1], center5[1]]);
xx5:makelist (realpart(rhs(c5[1][2])), i, 1, 1);
yy5:makelist (imagpart(rhs(c5[1][2])), i, 1, 1);
for n:2 thru nMax5 step 1 do /* all components in 1 list */
block
(
c5:mnewton([e51, e52-w], [z,c], [center5[n], center5[n]]),
xx5:cons(realpart(rhs(c5[1][2])),xx5),
yy5:cons(imagpart(rhs(c5[1][2])),yy5)
);
/* ------------*/
for i:1 thru iMax step 1 do
block
(
t:t+dt,
w:rectform(ev(l(t), numer)), /* "exponential form prevents allroots from working", code by Robert P. Munafo */
/* period 1 */
c1:mnewton([e11, e12-w], [z,c], [center1[1], center1[1]]),
xx1:cons(realpart(rhs(c1[1][2])),xx1),
yy1:cons(imagpart(rhs(c1[1][2])),yy1),
/* period 2 */
c2:mnewton([e21, e22-w], [z,c], [center2[1], center2[1]]),
xx2:cons(realpart(rhs(c2[1][2])),xx2),
yy2:cons(imagpart(rhs(c2[1][2])),yy2),
/* period 3*/
for n:1 thru nMax3 step 1 do
block
( c3:mnewton([e31, e32-w], [z,c], [center3[n], center3[n]]),
xx3:cons(realpart(rhs(c3[1][2])),xx3),
yy3:cons(imagpart(rhs(c3[1][2])),yy3)
),
/* period 4 */
if evenp(i) then
for n:1 thru nMax4 step 1 do
block
( c4:mnewton([e41, e42-w], [z,c], [center4[n], center4[n]]),
xx4:cons(realpart(rhs(c4[1][2])),xx4),
yy4:cons(imagpart(rhs(c4[1][2])),yy4)
),
/* period 5 */
if evenp(i) then
for n:1 thru nMax5 step 1 do /* all components in 1 list */
block
( c5:mnewton([e51, e52-w], [z,c], [center5[n], center5[n]]),
xx5:cons(realpart(rhs(c5[1][2])),xx5),
yy5:cons(imagpart(rhs(c5[1][2])),yy5)
)
);
stop:elapsed_run_time ();
time:fix(stop-start);
nMax:nMax1+nMax2+nMax3+nMax4+nMax5;
load(draw);
draw2d(
file_name = "c4n", /* file in directory C:\Program Files\Maxima-5.16.1\wxMaxima */
terminal = 'jpg, /* jpg when draw to file with jpg extension */
pic_width = 1000,
pic_height = 1000,
yrange = [-1.5,1.5],
xrange = [-2,1],
title= concat("Boundaries of ",string(nMax)," hyperbolic components of Mandelbrot set in ",string(time)," sec"),
xlabel = "c.re ",
ylabel = "c.im",
point_type = dot,
point_size = 5,
points_joined =true,
user_preamble="set size square;set key out vert;set key bot center",
color = black,
key = "one period 1 component ",
points(xx1,yy1),
key = "one period 2 component ",
color = green,
points(xx2,yy2),
points_joined =false,
color = red,
key = concat(string(nMax3)," period 3 components "),
points(xx3,yy3),
key = concat(string(nMax4)," period 4 components "),
points(xx4,yy4),
key = concat(string(nMax5)," period 5 components "),
points(xx5,yy5)
);
See also
- Other method of drawing based on boundary equations
- Centers of hyperbolic components computed with MPSolve
References
- ↑ WikiBooks/Fractals/Iterations in the complex plane/Mandelbrot set
- ↑ Robert P. Munafo - private communcation
- ↑ Maxima Manual: 63. mnewton
- ↑ Mark McClure "Bifurcation sets and critical curves" - Mathematica in Education and Research, Volume 11, issue 1 (2006). kopia archiwizowana w Wayback Machine
- ↑ jtroot3 Maxima package by Raymond Toy kopia archiwizowana w Wayback Machine
- ↑ cvs /maxima/share/numeric/jtroot3.mac
- ↑ Maxima Manual: 21. function allroots
- ↑ Robert P. Munafo - private communcation
- ↑ Maxima draw package by Mario Rodríguez Riotorto kopia archiwizowana w Wayback Machine
Acknowledgements
This program is not only my work but was done with help of many great people (see references). Warm thanks (:-))
Licencja
- Wolno:
- dzielić się – kopiować, rozpowszechniać, odtwarzać i wykonywać utwór
- modyfikować – tworzyć utwory zależne
- Na następujących warunkach:
- uznanie autorstwa – musisz określić autorstwo utworu, podać link do licencji, a także wskazać czy utwór został zmieniony. Możesz to zrobić w każdy rozsądny sposób, o ile nie będzie to sugerować, że licencjodawca popiera Ciebie lub Twoje użycie utworu.
- na tych samych warunkach – Jeśli zmienia się lub przekształca niniejszy utwór, lub tworzy inny na jego podstawie, można rozpowszechniać powstały w ten sposób nowy utwór tylko na podstawie tej samej lub podobnej licencji.

|
Udziela się zgody na kopiowanie, rozpowszechnianie oraz modyfikowanie tego dokumentu zgodnie z warunkami GNU Licencji Wolnej Dokumentacji, w wersji 1.2 lub nowszej opublikowanej przez Free Software Foundation; bez niezmiennych sekcji, bez treści umieszczonych na frontowej lub tylnej stronie okładki. Kopia licencji załączona jest w sekcji zatytułowanej GNU Licencja Wolnej Dokumentacji.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
Podpisy
Obiekty przedstawione na tym zdjęciu
przedstawia
Jakaś wartość bez elementu Wikidanych
26 wrz 2008
image/jpeg
3b3138087aa5981d78362ded9a55c979d4b31d6e
59 769 bajt
1000 piksel
1000 piksel
Historia pliku
Kliknij na datę/czas, aby zobaczyć, jak plik wyglądał w tym czasie.
| Data i czas | Miniatura | Wymiary | Użytkownik | Opis | |
|---|---|---|---|---|---|
| aktualny | 18:54, 27 wrz 2008 |  | 1000 × 1000 (58 KB) | wikimediacommons>Soul windsurfer | {{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }} |
Lokalne wykorzystanie pliku
Poniższa strona korzysta z tego pliku: