Zbiór niezależny

Zbiór niezależny w grafie $G=(V,E)$ – zbiór wierzchołków $V^{\prime }\subseteq V,$ pomiędzy którymi nie ma żadnej krawędzi. Innymi słowy każda krawędź w $G$ jest incydentna z co najwyżej jednym wierzchołkiem w tym zbiorze.

Problem największego zbioru niezależnego polegający na znalezieniu w danym grafie zbioru niezależnego o maksymalnej liczbie wierzchołków, jest znanym problemem NP-trudnym.

Problem ten nie powinien być mylony z maksymalnym zbiorem niezależnym w sensie inkluzji. Zbiór taki jest maksymalny gdy dodanie do niego jakiegokolwiek elementu sprawia, że przestaje być niezależny. Znalezienie takiego zbioru wierzchołków jest proste i może być wykonane za pomocą algorytmu zachłannego.

• 
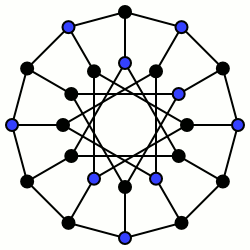
  9 zaznaczonych na niebiesko wierzchołków tworzy (zaskakująco asymetryczny) maksymalny zbiór niezależny w tym grafie o 24 wierzchołkach.

Zobacz też

• klika
• skojarzenie